2022-2023學年吉林省長春市榆樹市八號二中八年級（上）期末數學試卷

一.選擇題（每題3分共8小題24分）

• 1．8的立方根是（　　）

  A．2

  B．-2

  C．±2

  D．2 2
  組卷：466引用：61難度：0.9

  解析

• 2．下列長度的三條線段能構成直角三角形的是（　　）

  A．4，5，6

  B．6，8，10

  C．1，1，1

  D．5，12，23
  組卷：183引用：4難度：0.6

  解析

• 3．實數16的算術平方根是（　　）

  A．8

  B．±8

  C．4

  D．±4
  組卷：1428引用：13難度：0.8

  解析

• 4．用反證法證明命題“鈍角三角形中必有一個內角小于45°”時，首先應該假設這個三角形中（　　）

  A．有一個內角小于45°

  B．每一個內角都小于45°

  C．有一個內角大于等于45°

  D．每一個內角都大于等于45°
  組卷：1751引用：25難度：0.7

  解析

• 5．如圖是一所學校對學生上學方式進行調查后，根據調查結果繪制了一個不完整的統計圖，其中“其他”部分所對的圓心角度數是36°，則“步行”部分所占的百分比是（　　）

  A．36%

  B．40%

  C．45%

  D．50%
  組卷：322引用：7難度：0.6

  解析

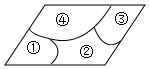• 6．小紅同學周末在家做家務，不慎把家里的一塊平行四邊形玻璃打碎成如圖所示的四塊，為了能從玻璃店配到一塊與原來相同的玻璃，他應該帶其中（　　）兩塊去玻璃店．

  A．①②

  B．②④

  C．②③

  D．①③
  組卷：518引用：3難度：0.7

  解析

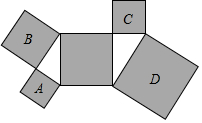• 7．如圖，所有陰影部分四邊形都是正方形，所有三角形都是直角三角形，若正方形A、B、D的面積依次為6、10、24，則正方形C的面積為（　　）

  A．4

  B．6

  C．8

  D．12
  組卷：2142引用：21難度：0.7

  解析

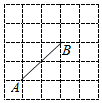• 8．如圖，在5×5的正方形網格中，每個小正方形的頂點稱為格點，點A、B均在格點上．要在格點上確定一點C，連結AC和BC，使△ABC是等腰三角形，則網格中滿足條件的點C的個數是（　　）

  A．5個

  B．6個

  C．7個

  D．8個
  組卷：392引用：4難度：0.8

  解析

三.解答題（共10小題共78分）

• 23．我們知道，任意一個正整數k都可以進行這樣的分解：k=m×n（m,n是正整數，且m≤n），在k的所有這種分解中，如果m,n兩因數之差的絕對值最小，我們就稱m×n是k的最佳分解，并規定：f（k）=

  m

  n

  ．例如：18可以分解成1×18，2×9或3×6，因為18-1＞9-2＞6-3，所以3×6是18的最佳分解，所以f（18）=

  3

  6

  =

  1

  2

  ．
  【探索規律】
  （1）f（20）=

  ；f（36）=

  ；
  （2）若x是正整數，猜想f（x²+2x）=

  ；
  【應用規律】
  （3）若f（x²+2x）=

  2021

  2022

  ，其中x是正整數，求x的值；
  （4）若f（x²-48）=1，其中x是正整數，所有x的值的和為

  ．
  組卷：789引用：3難度：0.3

  解析

• 24．如圖，在△ABC中，CA=CB，過點A作射線AP∥BC，點M、N分別在邊BC、AC上（點M、N不與所在線段端點重合），且BM=AN，連結BN并延長交射線AP于點D，連結MA并延長交AD的垂直平分線于點E，連結ED．
  【猜想】如圖①，當∠C=30°時，可證△BCN≌△ACM，從而得出∠CBN=∠CAM，進而得出∠BDE的大小為

  度．
  【探究】如圖②，若∠C=β．
  （1）求證：△BCN≌△ACM．
  （2）∠BDE的大小為

  度（用含β的代數式表示）．
  【應用】如圖③，當∠C=120°時，AM平分∠BAC，若AM、BN交于點F，DE=

  1

  2

  DF，DE=1，則△DEF的面積為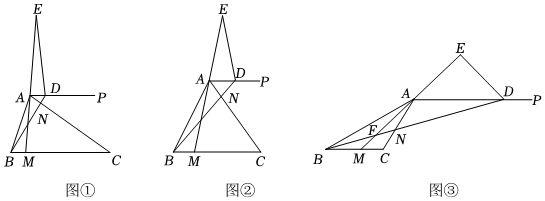

  ．
  
  組卷：248引用：2難度：0.4

  解析