2022-2023學年新疆烏魯木齊101中高二（上）期末數學試卷

一、選擇題（12題每題5分共60分）

• 1．設F₁、F₂分別為雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦點，若在雙曲線右支上存在點P，滿足|PF₂|=|F₁F₂|，且F₂到直線PF₁的距離等于雙曲線的實軸長，則該雙曲線的離心率e為（　　）

  A． 4 5

  B． 5 4

  C． 3 5

  D． 5 3
  組卷：1046引用：31難度：0.7

  解析

• 2．已知F是橢圓

  C

  ：

  x

  2

  4

  +

  y

  2

  3

  =

  1

  的左焦點，P為橢圓C上任意一點，點Q坐標為（1，1），則|PQ|+|PF|的最大值為（　　）

  A．3

  B．5

  C． 41

  D．13
  組卷：617引用：9難度：0.7

  解析

• 3．如圖，在斜棱柱ABCD-A₁B₁C₁D₁中，AC與BD的交點為點M，

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，則

  M

  C

  1

  =（　　）

  A． 1 2 a + 1 2 b + c

  B． - 1 2 a - 1 2 b - c

  C． - 1 2 a + 1 2 b + c

  D． - 1 2 a - 1 2 b + c
  組卷：1438引用：24難度：0.8

  解析

• 4．已知邊長為2的等邊三角形ABC，D是平面ABC內一點，且滿足DB：DC=2：1，則三角形ABD面積的最小值是（　　）

  A． 4 3 （ 3 - 1 ）

  B． 4 3 （ 3 + 1 ）

  C． 4 3 3

  D． 3 3
  組卷：100引用：6難度：0.5

  解析

• 5．在正方體ABCD-A₁B₁C₁D₁中，P為B₁D₁的中點，則直線PB與AD₁所成的角為（　　）

  A． π 2

  B． π 3

  C． π 4

  D． π 6
  組卷：5038引用：39難度：0.7

  解析

• 6．已知x,y∈R，向量

  a

  =

  （

  x

  ,

  1

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，

  y

  ,

  1

  ）

  ，

  c

  =

  （

  3

  ，-

  6

  ，

  3

  ）

  ，且

  a

  ⊥

  c

  ，

  b

  ∥

  c

  ，則

  |

  a

  +

  b

  |

  =（　　）

  A． 2 2

  B． 2 3

  C．4

  D．3
  組卷：587引用：25難度：0.7

  解析

• 7．若圓x²+y²=1上總存在兩個點到點（a,1）的距離為2，則實數a的取值范圍是（　　）

  A．（-2 2 ，0）∪（0，2 2 ）	B．（-2 2 ，2 2 ）
  C．（-1，0）∪（0，1）	D．（-1，1）
  組卷：412引用：12難度：0.6

  解析

三、解答題（共65分）

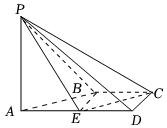• 20．如圖，在四棱錐P-ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD=

  1

  2

  AD=1．E為棱AD的中點，異面直線PA與CD所成的角為90°．
  （1）在平面PAB內是否存在一點M，使得直線CM∥平面PBE，如果存在，請確定點M的位置，如果不存在，請說明理由；
  （2）若二面角P-CD-A的大小為45°，求P到直線CE的距離．
  組卷：220引用：6難度：0.6

  解析

• 21．某校積極開展社團活動，在一次社團活動過程中，一個數學興趣小組發現《九章算術》中提到了“芻甍”這個五面體，于是他們仿照該模型設計了一道數學探究題，如圖1，E、F、G分別是正方形的三邊AB、CD、AD的中點，先沿著虛線段FG將等腰直角三角形FDG裁掉，再將剩下的五邊形ABCFG沿著線段EF折起，連接AB、CG就得到了一個“芻甍”（如圖2）．
  
  （1）若O是四邊形EBCF對角線的交點，求證：AO∥平面GCF；
  （2）若二面角A-EF-B的大小為

  2

  3

  π

  ，求直線AB與平面GCF所成角的正弦值．
  組卷：136引用：14難度：0.6

  解析