當(dāng)前位置：試卷中心 > 試卷詳情

2022-2023學(xué)年浙江省金華市東陽(yáng)市市北中學(xué)等四校九年級(jí)（下）期中數(shù)學(xué)試卷

發(fā)布：2024/4/23 12:26:7

一、選擇題（本題有10小題，每小題3分，共30分）

1．0.1的相反數(shù)是（　　）
A．0.1 B．-0.1 C．
1
10
D．10
組卷：39引用：1難度：0.8
解析
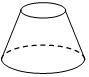2．下面立體圖形的左視圖是（　　）
A． B． C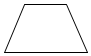． D．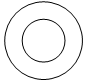
組卷：66引用：3難度：0.8
解析
3．在平面直角坐標(biāo)系中，點(diǎn)P（-3，2）關(guān)于x軸對(duì)稱的點(diǎn)的坐標(biāo)是（　　）
A．（3，2） B．（2，-3） C．（-3，2） D．（-3，-2）
組卷：523引用：11難度：0.9
解析
4．若根式
x
-
1
有意義，則x的取值范圍是（　　）
A．x＞1 B．x＜1 C．x≠1 D．x≥1
組卷：23引用：2難度：0.8
解析
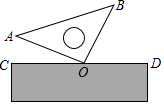5．如圖所示，將一塊直角三角板的直角頂點(diǎn)O放在直尺的一邊CD上，如果∠AOC=23°，那么∠BOD=（　　）
A．67° B．57° C．77° D．23°
組卷：204引用：2難度：0.7
解析

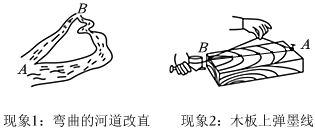6．生活中，有下列兩個(gè)現(xiàn)象，對(duì)于這兩個(gè)現(xiàn)象的解釋，正確的是（　　）

A．均用兩點(diǎn)之間線段最短來(lái)解釋

B．均用兩點(diǎn)確定一條直線來(lái)解釋

C．現(xiàn)象1用兩點(diǎn)之間線段最短來(lái)解釋，現(xiàn)象2用兩點(diǎn)確定一條直線來(lái)解釋

D．現(xiàn)象1用兩點(diǎn)確定一條直線來(lái)解釋，現(xiàn)象2用兩點(diǎn)之間線段最短來(lái)解釋

組卷：441引用：5難度：0.8

解析

7．幾個(gè)人打算合買一件物品．每人出12元，還少3元；每人出13元，就多12元，則總?cè)藬?shù)有（　　）
A．12人 B．13人 C．15人 D．16人
組卷：351引用：2難度：0.5
解析
8．按如圖所示的運(yùn)算程序，能使輸出的結(jié)果為26的是（　　）
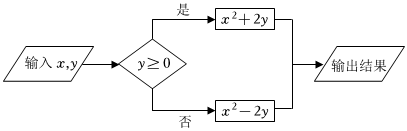
A．x=-2，y=-2 B．x=4，y=-5 C．x=-2，y=5 D．x=4，y=-2
組卷：97引用：1難度：0.7
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部?jī)?nèi)容及下載

三、解答題（本題有8小題，共66分，各小題都必須寫(xiě)出解答過(guò)程）

23．如圖1，在平面直角坐標(biāo)系中，拋物線y₀=-x²+bx+c與x軸交于點(diǎn)A（-4，0），點(diǎn)B（2，0），與y軸交于點(diǎn)C．
（1）求拋物線y₀的表達(dá)式及點(diǎn)C的坐標(biāo)；
（2）若點(diǎn)D₀是拋物線y₀上一動(dòng)點(diǎn)，連接CD₀，點(diǎn)D₀在拋物線y₀上運(yùn)動(dòng)時(shí)，
①取CD₀的中點(diǎn)D₁，當(dāng)點(diǎn)D₀與點(diǎn)A重合時(shí)，D₁的坐標(biāo)為
；當(dāng)點(diǎn)D₀與點(diǎn)B重合時(shí)，D₁的坐標(biāo)為
；請(qǐng)?jiān)趫D2的網(wǎng)格中畫(huà)出點(diǎn)D₁的運(yùn)動(dòng)軌跡，并猜想點(diǎn)D₁的運(yùn)動(dòng)軌跡是什么圖形：
；并求點(diǎn)D₁運(yùn)動(dòng)軌跡的函數(shù)y₁的解析式；
②在線段CD₁上取中點(diǎn)D₂，點(diǎn)D₂運(yùn)動(dòng)軌跡的函數(shù)的解析式為y₂，在線段CD₂上取中點(diǎn)D₃，點(diǎn)D₃的運(yùn)動(dòng)軌跡的函數(shù)的解析式為y₃，……，在線段CD_n-1上取中點(diǎn)D_n，點(diǎn)D_n的運(yùn)動(dòng)軌跡的函數(shù)的解析式為y_n（n為正整數(shù)）；請(qǐng)求出函數(shù)y_n的解析式（用含n的式子表示）．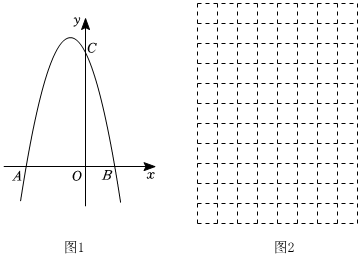
組卷：44引用：1難度：0.3
解析
24．在平面直角坐標(biāo)系中，點(diǎn)O為原點(diǎn)，點(diǎn)A的坐標(biāo)為（-6，0）．如圖1，正方形OBCD的頂點(diǎn)B在x軸的負(fù)半軸上，點(diǎn)C在第二象限．現(xiàn)將正方形OBCD繞點(diǎn)O順時(shí)針旋轉(zhuǎn)角α得到正方形OEFG．
（1）如圖2，若α=60°，OE=OA，求直線EF的函數(shù)表達(dá)式．
（2）若α為銳角，tanα=
1
2
，當(dāng)AE取得最小值時(shí)，求正方形OEFG的面積．
（3）當(dāng)正方形OEFG的頂點(diǎn)F落在y軸上時(shí)，直線AE與直線FG相交于點(diǎn)P，△OEP的其中兩邊之比能否為
2
：1？若能，求點(diǎn)P的坐標(biāo)；若不能，試說(shuō)明理由
組卷：2530引用：5難度：0.1
解析