2022-2023學年云南省德宏州高三（上）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．設集合U={0，1，2，3}，A={0，1，3}，B={1，2}，則A∩（?_UB）=（　　）

  A．{0，3}

  B．{1，3}

  C．{1}

  D．{0}
  組卷：139引用：4難度：0.9

  解析

• 2．若復數

  a

  +

  i

  1

  -

  i

  為純虛數，則|2+ai|等于（　　）

  A． 3

  B． 5

  C．3

  D．5
  組卷：207引用：3難度：0.8

  解析

• 3．在△ABC中，若AD為BC邊上的中線，點E在AD上，且AE=2ED，則

  EB

  =（　　）

  A． 2 3 AB - 1 3 AC

  B． 2 3 AC - 1 3 AB

  C． 7 6 AB - 5 6 AC

  D． 7 6 AC - 5 6 AB
  組卷：384引用：15難度：0.8

  解析

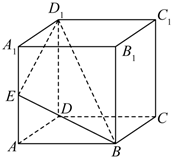• 4．如圖所示，在正方體ABCD-A₁B₁C₁D₁中，如果點E是AA₁的中點，那么過點D₁、B、E的截面圖形為（　　）

  A．三角形

  B．矩形

  C．正方形

  D．菱形
  組卷：677引用：7難度：0.6

  解析

• 5．若直線

  y

  =

  1

  2

  x

  +

  b

  是曲線y=lnx（x＞0）的一條切線，則實數b等于（　　）

  A．1+ln2

  B．-1+ln2

  C．ln2

  D．1
  組卷：249引用：2難度：0.7

  解析

• 6．已知函數y=f（x）的周期為2，當x∈[-1，1]時，f（x）=2^|x|-1．如果F（x）=f（x）-|log₅x|，那么F（x）的零點個數是（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：67引用：3難度：0.5

  解析

• 7．已知拋物線y²=4x的焦點為F，直線y=kx-2與拋物線交于兩個不同的點A，B．如果|AF|，2，|BF|成等差數列，那么k等于（　　）

  A．-1

  B．2

  C． 1 ± 3

  D． 1 + 3
  組卷：34引用：2難度：0.7

  解析

四、解答題：本題共6個小題，共70分。解答應寫出文字說明，證明過程或演算步驟。

• 21．已知雙曲線C₁：

  x

  2

  m

  2

  -

  y

  2

  n

  2

  =1（m＞0，n＞0）的焦點F到漸近線y=

  3

  x的距離為2

  3

  ．如果雙曲線C₁的頂點和焦點分別是橢圓C₂的焦點和頂點．
  （1）求橢圓C₂的方程；
  （2）設橢圓C₂的左右焦點分別是F₁、F₂，點P為橢圓上一點，過點P作x軸的垂線（不過點F₂）交橢圓C₂于點N，連接PF₂延長交橢圓于點Q，連接NQ．試判斷直線NQ是否過定點，如果過定點，求出定點坐標；如果不過定點，請說明理由．
  組卷：43引用：2難度：0.5

  解析

• 22．已知函數f（x）=e^x-2，g（x）=lnx²+a.當a＞0時，g（x）-f（x）在（0，+∞）上的最大值為ln4．
  （1）求實數a的值；
  （2）?x∈（0，+∞），有f（x+2-m）≥kx+k-1≥

  1

  2

  g

  （

  x

  e

  ）

  ．當k＞0時，求mk-k²的最大值．
  組卷：25引用：1難度：0.3

  解析