2022-2023學年上海市寶山中學高一（下）月考數學試卷（3月份）

一、填空題（本大題共有12小題，滿分36分）

• 1．已知tanα=3，則tan（α+

  π

  4

  ）=

   

  ．
  組卷：243引用：12難度：0.7

  解析

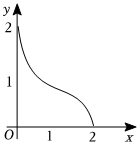• 2．觀察函數y=f（x），x∈[0，2]的圖像，寫出它的值域為

  ．
  組卷：197引用：2難度：0.9

  解析

• 3．函數

  y

  =

  1

  log

  5

  （

  2

  x

  -

  1

  ）

  的定義域是

  ．
  組卷：46引用：4難度：0.7

  解析

• 4．若函數f（x）=x²+（m-2）x+1為偶函數，則m的值為

  ．
  組卷：49引用：2難度：0.8

  解析

• 5．已知全集U=R，集合A={y|y=2^x，x∈R}，則

  A

  =

  .?
  組卷：35引用：1難度：0.9

  解析

• 6．已知α終邊過點P（1，a），若

  sinα

  =

  -

  6

  3

  ，則tanα=

  ．
  組卷：133引用：2難度：0.7

  解析

• 7．設奇函數f（x）的定義域為[-4，4]，若當x∈[-4，0]時，f（x）的圖象如圖，則不等式f（x）＜0的解是

  ．
  組卷：34引用：2難度：0.7

  解析

三、解答題（本大題滿分0分）

• 20．已知定義域為R的函數

  f

  （

  x

  ）

  =

  1

  -

  2

  x

  2

  x

  +

  1

  +

  a

  是奇函數．
  （1）求a的值；
  （2）判斷f（x）的單調性，并證明；
  （3）若關于m的不等式f（-2m²+3m-4）+f（m²-2mt）≤0在m∈[1，3]上有解，求實數t的取值范圍．
  組卷：76引用：2難度：0.5

  解析

• 21．若函數f（x）滿足：對于任意正數s、t,都有f（s）＞0，f（t）＞0，f（s）+f（t）＜f（s+t），則稱函數f（x）為“L函數”．
  （1）試判斷函數h（x）=x²是否是“L函數”；
  （2）若函數g（x）=2^x-1+a（2^-x-1）為“L函數”，求實數a的取值范圍；
  （3）若函數f（x）為“L函數”，且f（1）=1，求證：對任意x∈（2^k-1，2^k）（k∈N^*），都有f（x）＞

  x

  2

  ．
  組卷：23引用：2難度：0.5

  解析