當前位置：試卷中心 > 試卷詳情

2022-2023學年四川省成都七中八一學校八年級（上）第一次月考數學試卷

發布：2024/4/20 14:35:0

一、單選題（每小題4分，共32分）

1．在下列實數中，屬于無理數的是（　　）
A．0 B．
22
7
C．
9
D．
π
2
組卷：1258引用：23難度：0.9
解析
2．下列二次根式中，屬于最簡二次根式的是（　　）
A．
12
B．
2
C．
1
3
D．
0
.
1
組卷：464引用：7難度：0.9
解析
3．下列給出的四組數中，是勾股數的一組是（　　）
A．2，4，6 B．1，
3
，2
C．8，15，17 D．0.3，0.4，0.5
組卷：922引用：9難度：0.6
解析
4．若方程（a-6）x^|a|-5+5y=1是關于x,y的二元一次方程，則a的值為（　　）
A．±6 B．-6 C．±5 D．5
組卷：864引用：3難度：0.8
解析
5．成語“五雀六燕”出自中國古代數學名著《九章算術》第八卷《方程》中一道名題．原題為：“今有五雀、六燕，集稱之衡，雀俱重，燕俱輕．一雀一燕交而處，衡適平．并燕、雀重一斤．問燕、雀一枚各重幾何？”譯文為：“今有5只雀、6只燕，分別聚集而且用衡器稱之，聚在一起的雀重，燕輕．將一只雀、一只燕交換位置而放，重量相等．5只雀、6只燕重量為1斤．問雀、燕每只各多重？”現設每只雀x斤，每只燕y斤，則可列出方程組（　　）
A．
5
x
+
6
y
=
1
4
y
+
x
=
5
x
+
y
B．
5
y
+
6
x
=
1
4
x
+
y
=
5
y
+
x
C．
5
x
+
6
y
=
1
4
x
+
y
=
5
y
+
x
D．
5
y
+
6
x
=
1
4
y
+
x
=
5
x
+
y
組卷：430引用：11難度：0.7
解析
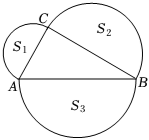6．如圖，分別以直角三角形的三邊為直徑向三角形外作三個半圓，圖中的字母是它們的面積其中S₂=6π，S₃=10π，則S₁為（　　）
A．8π B．4π C．16π D．4
組卷：1379引用：6難度：0.7
解析
7．方程組
2
x
+
y
=■
x
+
y
=
3
的解為
x
=
2
y
=■
，則被遮蓋的前后兩個數分別為（　　）
A．1、2 B．1、5 C．5、1 D．2、4
組卷：5644引用：51難度：0.8
解析
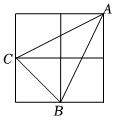8．如圖，小正方形邊長為1，連接小正方形的三個頂點，可得△ABC，則AC邊上的高是（　　）
A．
3
2
2
B．
5
5
10
C．
3
5
5
D．
4
5
5
組卷：2139引用：6難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

二、解答題（每小題8分，共20分）

25．（1）問題再現：學習二次根式時，老師給同學們提出了一個求代數式最小值的問題，如，“求代數式
x
2
+
4
+
（
12
-
x
）
2
+
9
的最小值”：小強同學發現
x
2
+
4
可看作兩直角邊分別為x和2的直角三角形斜邊長，
（
12
-
x
）
2
+
9
可看作兩直角邊分別是12-x和3的直角三角形的斜邊長．于是構造出如圖，將問題轉化為求線段AB的長，進而求得
x
2
+
4
+
（
12
-
x
）
2
+
9
的最小值是
．
（2）類比遷移：已知a,b均為正數，且a-b=4．求
a
2
+
4
-
b
2
+
1
的最大值．
（3）方法應用：已知a,b均為正數，且
4
a
2
+
b
2
，
9
a
2
+
b
2
，
a
2
+
4
b
2
是三角形的三邊長，求這個三角形的面積（用含a,b的代數式表示）．
組卷：726引用：3難度：0.2
解析
26．如圖1，在△ABC和△ADE中，∠DAE=∠BAC，AD=AE，AB=AC．
（1）求證：△ABD≌△ACE；
（2）如圖2，在△ABC和△ADE中，∠DAE=∠BAC，AD=AE，AB=AC，∠ADB=90°，點E在△ABC內，延長DE交BC于點F，求證：點F是BC中點；
（3）△ABC為等腰三角形，∠BAC=120°，AB=AC，點P為△ABC所在平面內一點，∠APB=120°，AP=2，BP=4，求CP的長．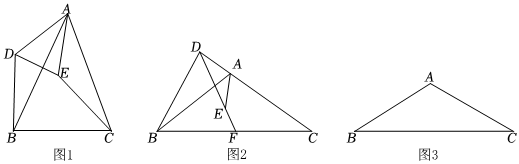
組卷：414引用：2難度：0.4
解析