2022年浙江省紹興市柯橋區高考數學方向性試卷（選考）（5月份）

一、選擇題：本大題共10小題，每小題4分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={x∈R|x≤0}，B={x∈R|-1≤x≤1}，則?_R（A∪B）=（　　）

  A．（-∞，0）

  B．[-1，0]

  C．[0，1]

  D．（1，+∞）
  組卷：168引用：4難度：0.9

  解析

• 2．人們對數學研究的發展一直推動著數域的擴展，從正數到負數、從整數到分數、從有理數到實數等等．16世紀意大利數學家卡爾丹和邦貝利在解方程時，首先引進了i²=-1，17世紀法因數學家笛卡兒把i稱為“虛數”，用a+bi（a、b∈R）表示復數，并在直角坐標系上建立了“復平面”．若復數z滿足方程z²+2z+5=0，則z=（　　）

  A．-1+2i

  B．-2-i

  C．-1±2i

  D．-2±i
  組卷：102引用：2難度：0.7

  解析

• 3．已知橢圓

  C

  ：

  x

  2

  4

  +

  y

  2

  =

  λ

  （

  λ

  ＞

  0

  ）

  ，則該橢圓的離心率e=（　　）

  A． 3 3

  B． 1 2

  C． 3 2

  D． 5 2
  組卷：194引用：2難度：0.5

  解析

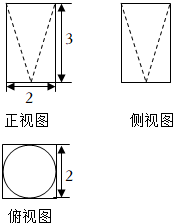• 4．已知某幾何體的三視圖如圖所示，則該幾何體的體積為（　　）

  A． 12 - 2 3 π

  B．12-π

  C．12-2π

  D．12-3π
  組卷：102引用：3難度：0.6

  解析

• 5．圖中的函數圖象所對應的解析式可能是（　　）

  A． y = - 1 2 | x - 1 |

  B． y = - | 1 2 x - 1 |

  C．y=-2|x-1|

  D．y=-|2x-1|
  組卷：157引用：2難度：0.8

  解析

• 6．若實數x,y滿足的約束條件

  x + 1 ≥ 0

  x + y + 1 ≥ 0

  x - y - 2 ≤ 0

  ，則

  z

  =

  y

  +

  3

  x

  的取值范圍是（　　）

  A．[-3，1）	B．（-∞，-3]∪（1，+∞）
  C．[-3，3]	D．（-∞，-3]∪[3，+∞）
  組卷：174引用：1難度：0.6

  解析

• 7．在△ABC中，“A＞B”是“cos2A＜cos2B”的（　　）

  A．充要條件	B．必要不充分條件
  C．充分不必要條件	D．既不充分又不必要條件
  組卷：190引用：5難度：0.5

  解析

三、解答題：本大題共5小題，共74分，解答應寫出文字說明、證明過程或演算步驟．

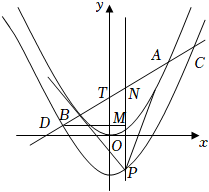• 21．如圖，已知拋物線C：x²=4y,直線l過點T（0，t）（t＞0）與拋物線交于A、B兩點，且在A、B處的切線交于點P，過點P且垂直于x軸的直線l'分別交拋物線C、直線l于M、N兩點．直線l與曲線C'：x²=4（y+t）交于C、D兩點．
  （Ⅰ）求證：點N是AB中點；
  （Ⅱ）設△DMN、△PAB的面積分別為S₁、S₂，求

  S

  1

  S

  2

  的取值范圍．
  組卷：131引用：1難度：0.2

  解析

• 22．設a為實數，函數f（x）=ae^x+xlnx+1．
  （Ⅰ）當

  a

  =

  -

  1

  e

  上時，求函數f（x）的單調區間；
  （Ⅱ）判斷函數f（x）零點的個數．
  組卷：164引用：1難度：0.2

  解析