2022-2023學(xué)年上海市靜安區(qū)市北中學(xué)高一（下）期中數(shù)學(xué)試卷

一、填空題（1-5每小題3分，6-10每小題3分，共35分）

• 1．在△ABC中，已知a=7，b=8，c=13，則角C的大小為

  ．
  組卷：69引用：5難度：0.7

  解析

• 2．已知cos（α-β）cosα+sin（α-β）sinα=-

  4

  5

  ，且β是第三象限的角，則sinβ=

   

  ．
  組卷：94引用：2難度：0.9

  解析

• 3．函數(shù)

  y

  =

  cos

  x

  3

  的最小正周期是

  ．
  組卷：28引用：1難度：0.8

  解析

• 4．函數(shù)

  y

  =

  tan

  （

  π

  6

  x

  +

  π

  3

  ）

  的定義域是

  ．
  組卷：155引用：2難度：0.8

  解析

• 5．角α的頂點(diǎn)在直角坐標(biāo)系的原點(diǎn)，始邊與x軸的正半軸重合，點(diǎn)M（x,1）是角α終邊上一點(diǎn)，若

  sinα

  =

  1

  3

  ，則x=

  ．
  組卷：16引用：1難度：0.7

  解析

• 6．已知

  2

  sinα

  +

  3

  cosα

  sinα

  -

  2

  cosα

  =

  1

  4

  ，則tanα的值為

  ．
  組卷：243引用：6難度：0.9

  解析

三、解答題（共49分）

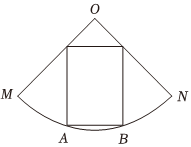• 17．如圖，有一塊扇形草地OMN，已知半徑為R，∠MON=

  π

  2

  ，現(xiàn)要在其中圈出一塊矩形場(chǎng)地ABCD作為兒童樂(lè)園使用，其中點(diǎn)A，B在弧MN上，且線段AB平行于線段MN；
  （1）若點(diǎn)A為弧MN的一個(gè)三等分點(diǎn)，求矩形ABCD的面積S；
  （2）設(shè)

  ∠

  AOB

  =

  θ

  （

  0

  ＜

  θ

  ＜

  π

  2

  ）

  ，當(dāng)A在何處時(shí)，矩形ABCD的面積S最大？最大值為多少？
  組卷：134引用：6難度：0.6

  解析

• 18．在△ABC中，∠CAB=120°．
  （1）如圖1，若點(diǎn)P為△ABC的重心，試用

  AB

  、

  AC

  表示

  AP

  ；
  （2）如圖2，若點(diǎn)P在以A為圓心，AB為半徑的圓弧

  ?

  BC

  上運(yùn)動(dòng)（包含B、C兩個(gè)端點(diǎn)），且AB=AC=1，設(shè)

  AP

  =

  λ

  AB

  +

  μ

  AC

  （λ，μ∈R），求λμ的取值范圍；
  （3）如圖3，若點(diǎn)P為△ABC外接圓的圓心，設(shè)

  AP

  =m

  AB

  +n

  AC

  （m,n∈R），求m+n的最小值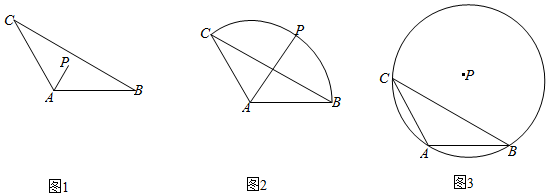
  
  組卷：263引用：3難度：0.4

  解析