當前位置：試卷中心 > 試卷詳情

2023-2024學年山東省東營市廣饒縣八年級（上）期中數學試卷（五四學制）

發布：2024/9/30 5:0:1

一、選擇題（本大題共10小題，共30.0分。在每小題列出的選項中，選出符合題目的一項）

1．下列各式中，分式的個數為（　　）
x
-
y
3
，
a
2
x
-
1
，
x
π
+
1
，-
3
a
b
，
1
2
x
+
y
，
1
2
x
+
y
,
2
x
-
2
=
1
x
+
3
；
A．5個 B．4個 C．3個 D．2個
組卷：1448引用：28難度：0.9
解析
2．下列運算中，錯誤的是（　　）
A．
ac
bc
=
a
b
B．
-
a
-
b
a
+
b
=
-
1
C．
0
.
5
a
+
b
0
.
2
a
-
0
.
3
b
=
5
a
+
10
b
2
a
-
3
b
D．
a
b
=
ac
bc
組卷：199引用：2難度：0.5
解析
3．下列各多項式中，不能用平方差公式分解的是（　　）
A．a²b²-1 B．4-0.25a² C．-a²-b² D．-x²+1
組卷：596引用：11難度：0.9
解析
4．某班要推選學生參加學校的“詩詞達人”比賽，有7名學生報名參加班級選拔賽，他們的選拔賽成績各不相同，現取其中前3名參加學校比賽．小紅要判斷自己能否參加學校比賽，在知道自己成績的情況下，還需要知道這7名學生成績的（　　）
A．眾數 B．中位數 C．平均數 D．方差
組卷：145引用：3難度：0.9
解析
5．已知一組數據a,b,c的平均數為5，方差為4，那么數據a-2，b-2，c-2的平均數和方差分別是（　　）
A．3，2 B．3，4 C．5，2 D．5，4
組卷：2470引用：30難度：0.9
解析
6．把分式
x
2
+
y
2
10
xy
中的x、y都擴大為原來的5倍，分式的值（　　）
A．不變 B．擴大5倍 C．縮小為
1
5
D．擴大25倍
組卷：204引用：4難度：0.9
解析
7．當n為自然數時，（n+1）²-（n-3）²一定能（　　）
A．被5整除 B．被6整除 C．被7整除 D．被8整除
組卷：3027引用：10難度：0.7
解析
8．如果x²+2（m-3）x+16是完全平方式，那么m的值為（　　）
A．5或1 B．7或-1 C．5 D．7
組卷：601引用：6難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本大題共3小題，共40分。解答應寫出文字說明，證明過程或演算步驟）

25．教科書中這樣寫道：“形如a²±2ab+b²的式子稱為完全平方式”，如果一個多項式不是完全平方式，我們常做如下變形：先添加一個適當的項，使式子中出現完全平方式，再減去這個項，使整個式子的值不變，這種方法叫做配方法．配方法是一種重要的解決問題的數學方法，不僅可以將一個看似不能分解的多項式分解因式，還能解決一些與非負數有關的問題或求代數式最大值、最小值等問題．
例如：分解因式：x²+2x-3．
解：原式=x²+2x+1-1-3=（x+1）²-4=（x+1+2）（x+1-2）=（x+3）（x-1）；
再如：求代數式2x²+4x-6的最小值．
解：2x²+4x-6=2（x²+2x-3）=2（x²+2x+1-1-3）=2[（x+1）²-4]=2（x+1）²-8；
∵（x+1）²≥0，
∴原式≥-8，
即當x=-1時，原式有最小值-8．
學以致用：
（1）用配方法分解因式：x²-4x-5；（其他方法不得分）
（2）用配方法求多項式-2x²-8x+5的最大值？并求出此時x的值．
組卷：456引用：3難度：0.6
解析

四、附加題：

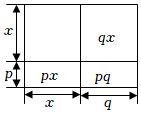26．結合圖，觀察下列式子：
（x+p）（x+q）=x²+px+qx+pq
=x²+（p+q）x+pq
于是有：x²+（p+q）x+pq=（x+p）（x+q）．
（1）填空：因式分解x²+5x+6=（x+
）（x+
）；
（2）化簡：
（
x
2
-
x
-
2
x
2
-
4
x
+
4
-
2
x
+
6
x
2
+
x
-
6
）
÷
x
x
-
2
；
（3）化簡：
1
x
2
+
x
+
1
x
2
+
3
x
+
2
+
1
x
2
+
5
x
+
6
+
1
x
2
+
7
x
+
12
．
組卷：516引用：3難度：0.5
解析