2022-2023學(xué)年四川省南充市高坪區(qū)白塔中學(xué)高一（下）月考數(shù)學(xué)試卷（5月份）

一．單選題（本題共8個小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合要求的.）

• 1．已知：sinθ=

  1

  3

  ，θ在第二象限，那么cosθ=（　　）

  A． 1 3

  B．- 1 3

  C． 2 2 3

  D．- 2 2 3
  組卷：283引用：3難度：0.9

  解析

• 2．將正弦函數(shù)f（x）=sinx的圖象先向左平移

  π

  3

  個單位長度，再將得到的圖象上所有點的橫坐標(biāo)縮短到原來的

  1

  2

  ，縱坐標(biāo)不變，最后得到函數(shù)g（x）的圖象，則g（x）=（　　）

  A． g （ x ） = sin （ 2 x + 2 π 3 ）	B． g （ x ） = sin （ 2 x + π 3 ）
  C． g （ x ） = sin （ x 2 + π 3 ）	D． g （ x ） = sin （ x 2 + π 6 ）
  組卷：860引用：7難度：0.9

  解析

• 3．對于非零向量

  a

  ，

  b

  ，“

  a

  +

  b

  =

  0

  ”是“

  a

  ∥

  b

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：658引用：28難度：0.9

  解析

• 4．下列區(qū)間中，函數(shù)

  f

  （

  x

  ）

  =

  2

  sin

  （

  x

  +

  π

  3

  ）

  單調(diào)遞增的是（　　）

  A． （ 0 ， π 6 ）

  B． （ π 6 ， π 2 ）

  C． （ π 2 ， 2 π 3 ）

  D． （ π 3 ， π 2 ）
  組卷：114引用：2難度：0.7

  解析

• 5．化簡：

  2

  sin

  （

  π

  -

  α

  ）

  +

  sin

  2

  α

  2

  cos

  2

  α

  2

  =（　　）

  A．sinα

  B．sin2α

  C．2sinα

  D． sin α 2
  組卷：78引用：3難度：0.7

  解析

• 6．已知P是邊長為2的正六邊形ABCDEF內(nèi)的一點，則

  AP

  ?

  AB

  的取值范圍是（　　）

  A．（-2，6）

  B．（-6，2）

  C．（-2，4）

  D．（-4，6）
  組卷：7490引用：40難度：0.5

  解析

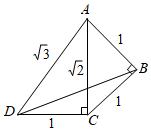• 7．如圖是公元前約400年古希臘數(shù)學(xué)家泰特托斯用來構(gòu)造無理數(shù)

  2

  ，

  3

  ，

  5

  ，…的圖形之一，此圖形中∠BAD的余弦值是（　　）

  A． 4 - 3 6

  B． 4 + 3 6

  C． 2 3 - 6 6

  D． 2 3 + 6 6
  組卷：114引用：5難度：0.8

  解析

四、解答題（本題共6個小題，17題10分，18-22題每題12分，共70分.解答題應(yīng)寫出文字說明、證明過程或演算步驟.）

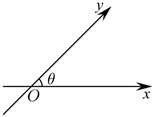• 21．如圖，數(shù)軸x,y的交點為O，夾角為θ，與x軸、y軸正向同向的單位向量分別是

  e

  1

  ，

  e

  2

  ．由平面向量基本定理，對于平面內(nèi)的任一向量

  OP

  ，存在唯一的有序?qū)崝?shù)對（x,y），使得

  OP

  =

  x

  e

  1

  +

  y

  e

  2

  ，我們把（x,y）叫做點P在斜坐標(biāo)系xOy中的坐標(biāo)（以下各點的坐標(biāo)都指在斜坐標(biāo)系xOy中的坐標(biāo)）．
  （1）若

  θ

  =

  90

  °

  ，

  OP

  為單位向量，且

  OP

  與

  e

  1

  的夾角為120°，求點P的坐標(biāo)；
  （2）若θ=45°，點P的坐標(biāo)為

  （

  1

  ，

  2

  ）

  ，求向量

  OP

  與

  e

  1

  的夾角的余弦值．
  組卷：194引用：7難度：0.5

  解析

• 22．已知

  f

  （

  x

  ）

  =

  lo

  g

  2

  （

  1

  x

  +

  a

  ）

  ，

  a

  ∈

  R

  ．
  （1）當(dāng)a=1時，解不等式f（x）＞1；
  （2）若關(guān)于x的方程

  f

  （

  x

  ）

  +

  lo

  g

  2

  x

  2

  =

  0

  的解集中恰好有一個元素，求實數(shù)a的值；
  （3）若對任意

  t

  ∈

  [

  1

  2

  ，

  3

  2

  ]

  ，函數(shù)f（x）在區(qū)間[t,t+1]上總有意義，且最大值與最小值的差不小于2，求a的取值范圍．
  組卷：376引用：3難度：0.3

  解析