2022-2023學年廣東省梅州市豐順縣東留中學八年級(上)月考數學試卷(12月份)
發布:2024/8/26 4:0:8
一、選擇題(共10題,共30分)
-
1.已知a>0,b<0,那么點P(a,b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限 組卷:474引用:29難度:0.9 -
2.下列各組線段中,不能構成三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6 組卷:11引用:1難度:0.7 -
3.關于x的方程kx+b=3的解為x=7,則直線y=kx+b的圖象一定過點( )
A.(3,0) B.(7,0) C.(3,7) D.(7,3) 組卷:3560引用:12難度:0.7 -
 4.甲、乙兩車從A地出發,沿同一路線駛向B地.甲車先出發勻速駛向B地,40min后,乙車出發,勻速行駛一段時間后,在途中的貨站裝貨耗時半小時.由于滿載貨物,為了行駛安全,速度減少了50km/h,結果與甲車同時到達B地.甲乙兩車距A地的路程y(km)與乙車行駛時間x(h)之間的函數圖象如圖所示,則下列說法:
4.甲、乙兩車從A地出發,沿同一路線駛向B地.甲車先出發勻速駛向B地,40min后,乙車出發,勻速行駛一段時間后,在途中的貨站裝貨耗時半小時.由于滿載貨物,為了行駛安全,速度減少了50km/h,結果與甲車同時到達B地.甲乙兩車距A地的路程y(km)與乙車行駛時間x(h)之間的函數圖象如圖所示,則下列說法:
①a=4.5;②甲的速度是60km/h;③乙出發80min追上甲;④乙剛到達貨站時,甲距B地180km.其中正確的有( )A.1個 B.2個 C.3個 D.4個 組卷:2469引用:19難度:0.5 -
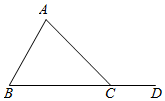 5.定理:三角形的一個外角等于與它不相鄰的兩個內角的和.
5.定理:三角形的一個外角等于與它不相鄰的兩個內角的和.
已知:如圖,∠ACD是△ABC的外角.求證:∠ACD=∠A+∠B.
下列說法正確的是( )證法1:如圖,
∵∠A+∠B+∠ACB=180°(三角形內角和定理),
又∵∠ACD+∠ACB=180°(平角定義),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代換).
∴∠ACD=∠A+∠B(等式性質).證法2:如圖,
∵∠A=76°,∠B=59°,
且∠ACD=135°(量角器測量所得)
又∵135°=76°+59°(計算所得)
∴∠ACD=∠A+∠B(等量代換).A.證法1還需證明其他形狀的三角形,該定理的證明才完整 B.證法1用嚴謹的推理證明了該定理 C.證法2用特殊到一般法證明了該定理 D.證法2只要測量夠一百個三角形進行驗證,就能證明該定理 組卷:1372引用:23難度:0.7 -
 6.快車從甲地駛往乙地,慢車從乙地駛往甲地,兩車同時出發并且在同一條公路上勻速行駛.圖中折線表示快、慢兩車之間的距離y(km)與它們的行駛時間x(h)之間的函數關系.小欣同學結合圖象得出如下結論:
6.快車從甲地駛往乙地,慢車從乙地駛往甲地,兩車同時出發并且在同一條公路上勻速行駛.圖中折線表示快、慢兩車之間的距離y(km)與它們的行駛時間x(h)之間的函數關系.小欣同學結合圖象得出如下結論:
①快車途中停留了0.5h;
②快車速度比慢車速度多20km/h;
③圖中a=340;
④快車先到達目的地.
其中正確的是( )A.①③ B.②③ C.②④ D.①④ 組卷:3827引用:29難度:0.6 -
7.一次函數y=(a2+1)x-a的圖象上有兩點A(-1,y1),B(-2,y2),則y1與y2的大小關系為( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能確定 組卷:725引用:4難度:0.7 -
8.小華和小剛兄弟兩個同時從家去同一所學校上學,速度都是每分鐘走50米.小華從家到學校走直線用了10分鐘,而小剛從家出發先去找小明再到學校(均走直線),小剛到小明家用了6分鐘,小明家到學校用了8分鐘,小剛上學走了個( )
A.銳角彎 B.鈍角彎 C.直角彎 D.不能確定 組卷:102引用:3難度:0.9
三、解答題(共8題,共62分)
-
24.已知E、F分別是AB、CD上的動點,P也為一動點.
(1)圖(1)若AB∥CD,求證:∠P=∠BEP+∠PFD.
(2)圖(2)若∠P=∠PFD-∠BEP,求證:AB∥CD.
(3)圖(3)AB∥CD,移動E、F,使∠EPF=90°,作∠PEG=∠BEP,求的值.∠AEG∠PFD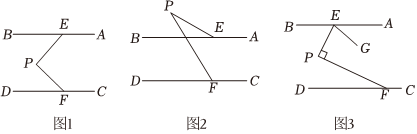 組卷:742引用:2難度:0.3
組卷:742引用:2難度:0.3 -
25.
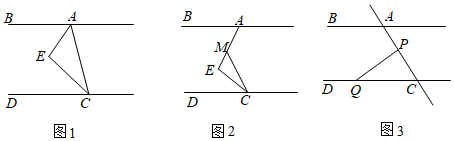
(1)特例發現:如圖1,AB∥CD,CE平分∠ACD,AE平分∠BAC.請觀察猜想∠AEC的度數并說明理由;
(2)類比探究:如圖2,點M是AE上一點,當∠E=90°保持不變,移動直角頂點E,使CE平分∠MCD.∠BAE與∠MCD存在怎樣的數量關系?并說明理由;
(3)拓展應用:如圖3,P為線段AC上一定點,點Q為直線CD上一動點,點Q不與點C重合.∠CPQ+∠CQP與∠BAC有何數量關系?猜想結論并說明理由.組卷:452引用:3難度:0.5


