當前位置：試卷中心 > 試卷詳情

2023年江蘇省揚州市邗江區世明雙語學校中考數學四模試卷

發布：2024/5/23 8:0:8

一.選擇題（共8小題，滿分24分，每小題3分）

1．下列運算正確的是（　　）
A．
12
-
3
=
3
B．（-3）²=6 C．3a⁴-2a²=a² D．（-a³）²=a⁵
組卷：238引用：4難度：0.9
解析
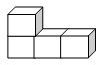2．如圖，圖中的幾何體中，它的左視圖是（　　）
A． B． C． D．
組卷：95引用：42難度：0.9
解析
3．下列二次根式中與
2
是同類二次根式的是（　　）
A．
12
B．
3
2
C．
2
3
D．
18
組卷：285引用：4難度：0.7
解析
4．
（
-
4
）
2
的值為（　　）
A．4 B．±4 C．2 D．±2
組卷：30引用：7難度：0.9
解析
5．下列調查中，適宜采用普查方式的是（　　）
A．了解一批圓珠筆的壽命
B．了解全國九年級學生身高的現狀
C．檢查神舟號載人飛船的各零部件
D．考查人們保護海洋的意識
組卷：106引用：3難度：0.9
解析
6．若關于x的分式方程
2
x
-
1
=
m
x
有正整數解，則整數m的值是（　　）
A．3 B．5 C．3或5 D．3或4
組卷：2375引用：14難度：0.7
解析
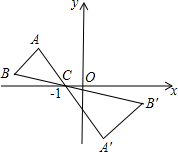7．如圖，△ABC中，A，B兩個頂點在x軸的上方，點C的坐標是（-1，0）．以點C為位似中心，在x軸的下方作△ABC的位似圖形，并把△ABC的邊長放大到原來的2倍，記所得的像是△A′B′C．設點B的對應點B′的橫坐標是a,則點B的橫坐標是（　　）
A．
-
1
2
a
B．
-
1
2
（
a
+
1
）
C．
-
1
2
（
a
-
1
）
D．
-
1
2
（
a
+
3
）
組卷：1792引用：58難度：0.5
解析
8．若一次函數y=ax+b與反比例函數y=
c
x
的圖象在第二象限內有兩個交點，且其中一個交點的橫坐標為-1，則二次函數y=ax²+bx-c的圖象可能是（　　）
A． B． C． D．
組卷：877引用：14難度：0.6
解析

二.填空題（共10小題，滿分30分，每小題3分）

9．代數式
x
x
+
2
在實數范圍內有意義，則實數x的取值范圍是
．
組卷：117引用：3難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三.解答題（共10小題，滿分96分）

27．我們定義：若一個三角形最大邊上的點將該邊分為兩條線段，且這兩條線段的積等于這個點到最大邊所對頂點連線的平方，則稱這個點為這個三角形的“比例中點”．例如：如圖1，已知鈍角△ABC中，∠ACB是鈍角，點D是AB上的一點，連接CD，若CD²=AD?BD，則稱點D是△ABC的“比例中點”．

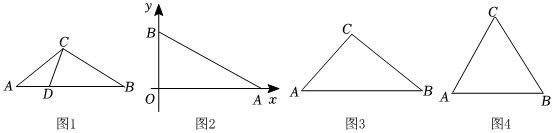
（1）如圖2，已知點A的坐標為（4，0），點B在y軸上，∠BAO=30°，若點M是△AOB的“比例中點”，則點M的坐標為
；
（2）如圖3，已知△ABC中，AB=28，∠A=45°，
tan
B
=
3
4
，若點N是△ABC的“比例中點”，求AN；
（3）如圖4，已知△ABC是等邊三角形，因為等邊三角形的三邊相等，所以其中任意一條邊都可以看成最大邊，試判斷等邊三角形有沒有“比例中點”？說明理由．
組卷：510引用：4難度：0.1
解析
28．如圖，二次函數y=
1
2
x²+bx+c與x軸交于O（0，0），A（4，0）兩點，頂點為C，連接OC、AC，若點B是線段OA上一動點，連接BC，將△ABC沿BC折疊后，點A落在點A′的位置，線段A′C與x軸交于點D，且點D與O、A點不重合．
（1）求二次函數的表達式；
（2）①求證：△OCD∽△A′BD；
②求
DB
BA
的最小值；
（3）當S_△OCD=8S_△A'BD時，求直線A′B與二次函數的交點橫坐標．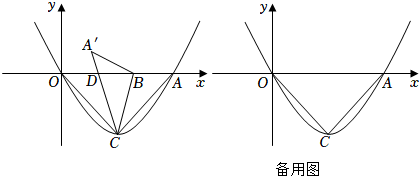
組卷：3795引用：9難度：0.1
解析