2023年安徽省蚌埠市蚌山區中考數學調研試卷

一、選擇題（本大題共6小題，共42分。在每小題列出的選項中，選出符合題目的一項）

• 1．有一些含有特殊數學規律的車牌號碼，如：皖C80808、皖C22222、皖C12321等，這些牌照中的五個數字都是關于中間的一個數字“對稱”的，給人以對稱的美的感受，我們不妨把這樣的牌照叫做“數字對稱”牌照．如果讓你負責制作只以8或9開頭且有五個數字的“數字對稱”牌照，那么最多可制作（　　）

  A．200個

  B．400個

  C．1000個

  D．2000個
  組卷：291引用：7難度：0.8

  解析

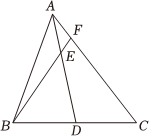• 2．AD是△ABC的中線，E是AD上一點，AE=

  1

  4

  AD，BE的延長線交AC于F，則

  AF

  AC

  的值為（　　）

  A． 1 4

  B． 1 5

  C． 1 6

  D． 1 7
  組卷：3938引用：16難度：0.7

  解析

• 3．設a為

  3

  +

  5

  -

  3

  -

  5

  的小數部分，b為

  6

  +

  3

  3

  -

  6

  -

  3

  3

  的小數部分．則

  2

  b

  -

  1

  a

  的值為（　　）

  A． 6 + 2 -1

  B． 6 - 2 +1

  C． 6 - 2 -1

  D． 6 + 2 +1
  組卷：6348引用：16難度：0.6

  解析

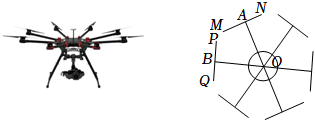• 4．如圖，是一架無人機俯視簡化圖，MN與PQ表示旋翼，旋翼長為24cm,A，B為旋翼的支點，各支點平分旋翼，飛行控制中心O到各旋翼支點的距離均為30cm,相鄰兩個支架的夾角均相等，當無人機靜止且支架與旋翼垂直時，M與P之間的距離為（　　）

  A．30-12 3

  B．30-12 5

  C．15-3 3

  D．15 5 -24
  組卷：421引用：2難度：0.3

  解析

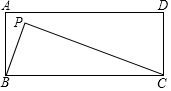• 5．如圖，矩形ABCD中，AB=3，BC=8，點P為矩形內一動點，且滿足∠PBC=∠PCD，則線段PD的最小值為（　　）

  A．5

  B．1

  C．2

  D．3
  組卷：1632引用：5難度：0.5

  解析

三、解答題（本大題共5小題，共80分。解答應寫出文字說明，證明過程或演算步驟）

• 14．如圖，在平面直角坐標系中，矩形ABCD的邊AB在x軸上，AB、BC的長分別是一元二次方程x²-7x+12=0的兩個根（BC＞AB），OA=2OB，邊CD交y軸于點E，動點P以每秒1個單位長度的速度，從點E出發沿折線段ED-DA向點A運動，運動的時間為t（0≤t＜6）秒，設△BOP與矩形AOED重疊部分的面積為S．
  （1）求點D的坐標；
  （2）求S關于t的函數關系式，并寫出自變量的取值范圍；
  （3）在點P的運動過程中，是否存在點P，使△BEP為等腰三角形？若存在，直接寫出點P的坐標；若不存在，請說明理由．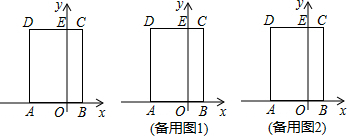
  
  組卷：862引用：5難度：0.4

  解析

• 15．問題提出：如圖1，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，⊙C半徑為2，P為圓上一動點，連接AP、BP，求AP+

  1

  2

  BP的最小值．
  （1）嘗試解決：為了解決這個問題，下面給出一種解題思路：如圖2，連接CP，在CB上取點D，使CD=1，則有

  CD

  CP

  =

  CP

  CB

  =

  1

  2

  ，又∵∠PCD=∠BCP，∴△PCD∽△BCP．∴

  PD

  BP

  =

  1

  2

  ，∴PD=

  1

  2

  BP，∴AP+

  1

  2

  BP=AP+PD．
  請你完成余下的思考，并直接寫出答案：AP+

  1

  2

  BP的最小值為

  ．
  （2）自主探索：在“問題提出”的條件不變的情況下，

  1

  3

  AP+BP的最小值為

  ．
  （3）拓展延伸：已知扇形COD中，∠COD=90°，OC=6，OA=3，OB=5，點P是

  ?

  CD

  上一點，求2PA+PB的最小值．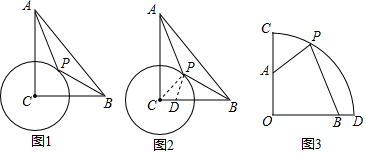
  
  組卷：5211引用：7難度：0.3

  解析