2022-2023學年黑龍江省雞西市雞東二中高三（上）期中數學試卷

一、選擇題

• 1．已知集合A={1，3，a²}，B={1，a+2}，若A∩B=B，則實數a的取值為（　　）

  A．1

  B．-1或2

  C．2

  D．-1或1
  組卷：145引用：9難度：0.9

  解析

• 2．設m,n表示不同的直線，α，β表示不同的平面，且m,n?α．則“α∥β”是“m∥β且n∥β”的（　　）

  A．充分但不必要條件	B．必要但不充分條件
  C．充要條件	D．既不充分又不必要條件
  組卷：1179引用：18難度：0.9

  解析

• 3．在等差數列{a_n}中，若a₂+a₈=8，則

  （

  a

  3

  +

  a

  7

  ）

  2

  -

  a

  5

  =（　　）

  A．4

  B．12

  C．56

  D．60
  組卷：210引用：2難度：0.7

  解析

• 4．設i為虛數單位，則復數

  5

  i

  -

  2

  =（　　）

  A．-2-i

  B．2-i

  C．2+i

  D． 5 4 - 1 4 i
  組卷：88引用：3難度：0.9

  解析

• 5．已知

  AB

  =

  （

  3

  ，

  4

  ）

  ，

  AC

  =

  （

  t

  ,

  6

  ）

  ，

  |

  BC

  |

  =

  2

  ，則

  AB

  ?

  BC

  =（　　）

  A．-6

  B．-8

  C．6

  D．8
  組卷：7引用：2難度：0.9

  解析

• 6．已知x,y,z∈R^*，滿足x-2y+3z=0，則

  y

  2

  xz

  的最小值是（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：245引用：5難度：0.7

  解析

• 7．已知lnx₁+2x₁-y₁+1=0，4x₂-y₂+3-ln2=0，則（x₁-x₂）²+（y₁-y₂）²的最小值為（　　）

  A． 17 ln 2 9

  B． 17 9

  C． 9 17

  D． 9 ln 2 17
  組卷：54引用：2難度：0.6

  解析

四、解答題

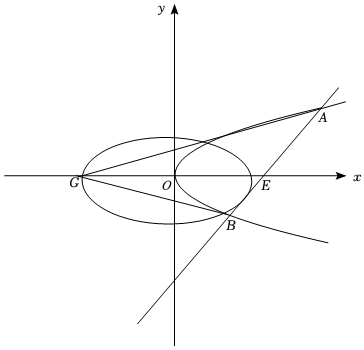• 21．已知平面直角坐標系中，點（4，0）到拋物線C₁：y²=2px（p＞0）準線的距離等于5，橢圓C₂：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  3

  2

  ，且過點

  （

  1

  ，

  3

  2

  ）

  ．
  （1）求C₁，C₂的方程；
  （2）如圖，過點E（m,0）（m＞2）作橢圓C₂的切線交C₁于A，B兩點，在x軸上取點G，使得∠AGE=∠BGE，試解決以下問題：
  ①證明：點G與點E關于原點中心對稱；
  ②若已知△ABG的面積是橢圓C₂四個頂點所圍成菱形面積的16倍，求切線AB的方程．
  組卷：282引用：3難度：0.5

  解析

• 22．處于信息化時代的現代社會，信號處理是非常關鍵的技術，而信號處理背后的“功臣”是數學中的正弦型函數．已知某一類型信號的波形可以用sinx和

  sin

  A

  x

  A

  （A∈N^*）進行疊加生成，即生成的波形對應函數解析式為f（x）=sinx+

  sin

  A

  x

  A

  ．
  （1）若A=3，討論f（x）在（0，π）上的單調性，并判斷其極值點的個數（提示：cos3x=-3cosx+4cos³x）；
  （2）若A=2，令g（x）=e^x，函數h（x）=f（x）-g（x），寫出函數h（x）的導函數h′（x）在（0，π）上的零點個數，并說明理由．
  組卷：33引用：2難度：0.3

  解析