2022-2023學年江西省宜春市樟樹市清江中學高一(下)期中數學試卷
發布:2024/7/4 8:0:9
一、單選題(每題5分,共40分)
-
1.已知點(1,2)在α的終邊上,則cosα=( )
A. 255B. 55C. 23D. 13組卷:228引用:4難度:0.8 -
2.已知向量
,a=(-1,2),若b=(3,λ)與a+2b平行,則實數λ的值為( )2a-bA. -23B. 23C.6 D.-6 組卷:325引用:7難度:0.7 -
3.cos78°cos18°+sin78°sin18°的值為( )
A. 12B. 13C. 32D. 33組卷:94引用:2難度:0.9 -
4.函數
的最小值和最小正周期分別是( )f(x)=cos(2x+π6)A. ,π-3B.-1,π C. ,2π-3D.-1,2π 組卷:213引用:3難度:0.9 -
5.將函數
的圖象上各點向右平移f(x)=3sin(13x+π12)個單位長度得函數g(x)的圖象,則g(x)的單調遞增區間為( )π12A. [2kπ-5π3,2kπ+22π3],k∈ZB. [4kπ-5π3,4kπ+4π3],k∈ZC. [6kπ-5π3,6kπ+4π3],k∈ZD.[4π,9π] 組卷:76引用:2難度:0.7 -
6.已知函數
在[0,π]上恰有3個零點,則ω的取值范圍是( )f(x)=2cos2ωx+3sin2ωx-1(ω>0)A. [1712,2312)B. (1712,2312]C. [2312,2912)D. (2312,2912]組卷:318引用:11難度:0.7 -
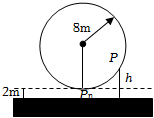 7.一個大風車的半徑為8m,12min旋轉一周,它的最低點P0離地面2m,風車翼片的一個端點P從P0開始按逆時針方向旋轉,則點P離地面距離h(m)與時間f(min)之間的函數關系式是( )
7.一個大風車的半徑為8m,12min旋轉一周,它的最低點P0離地面2m,風車翼片的一個端點P從P0開始按逆時針方向旋轉,則點P離地面距離h(m)與時間f(min)之間的函數關系式是( )A.h(t)=-8sin t+10π6B.h(t)=-cos t+10π6C.h(t)=-8sin t+8π6D.h(t)=-8cos t+10π6組卷:63引用:3難度:0.7
四、解答題(共70分)
-
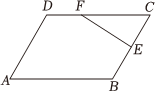 21.如圖,在平行四邊形ABCD中,∠BAD=60°,,BE=12BC.CF=2FD
21.如圖,在平行四邊形ABCD中,∠BAD=60°,,BE=12BC.CF=2FD
(1)若,求3x+2y的值;EF=xAB+yAD
(2)若,|AB|=6,求邊AD的長.AC?EF=-18組卷:58引用:5難度:0.5 -
22.已知O為坐標原點,對于函數f(x)=asinx+bcosx,稱向量
為函數f(x)的伴隨向量,同時稱函數f(x)為向量OM=(a,b)的伴隨函數.OM
(1)設函數,試求g(x)的伴隨向量的坐標;g(x)=sin(x+5π6)+cos(3π2+x)
(2)記向量的伴隨函數為f(x),當ON=(1,3)且f(x)=85時,求sinx的值;x∈(-π3,π6)
(3)設向量,λ∈R的伴隨函數為u(x),OP=(2λ,-2λ)的伴隨函數為v(x),記函數h(x)=u(x)+v2(x),求h(x)在[0,π]上的最大值.OQ=(1,1)組卷:62引用:6難度:0.5


