2023年山西大學附中中考數學二模試卷

一、選擇題（每題3分，本大題共10小題，共30分。在每小題列出的選項中，選出符合題目的一項）

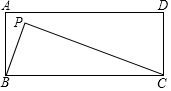• 1．如圖，矩形ABCD中，AB=3，BC=8，點P為矩形內一動點，且滿足∠PBC=∠PCD，則線段PD的最小值為（　　）

  A．5

  B．1

  C．2

  D．3
  組卷：1632引用：5難度：0.5

  解析

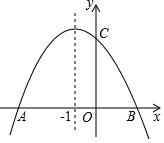• 2．如圖，拋物線y=ax²+bx+c（a≠0）交x軸于點A，B，交y軸于點C．若點A坐標為（-4，0），對稱軸為直線x=-1，則下列結論錯誤的是（　　）

  A．二次函數的最大值為a-b+c

  B．a+b+c＞0

  C．b2-4ac＞0

  D．2a+b=0
  組卷：2192引用：17難度：0.5

  解析

• 3．已知二次函數y=-x²+x+c（c＜0），當自變量為x₁時，其函數值y₁大于零；當自變量為x₁-1與x₁+1時，其函數值分別為y₂，y₃，則（　　）

  A．y2＞0，y3＞0

  B．y2＞0，y3＜0

  C．y2＜0，y3＜0

  D．y2＜0，y3＞0
  組卷：535引用：6難度：0.4

  解析

• 4．如圖，在⊙O中，AB是直徑，CD⊥AB，∠ACD=60°，OD=2，那么DC的長等于（　　）

  A． 3

  B． 2 3

  C．2

  D．4
  組卷：407引用：7難度：0.7

  解析

• 5．二次函數y=ax²+bx+c（a,b,c是常數，a≠0）的自變量x與函數值y的部分對應值如下表：

  x	…	-2	-1	0	1	2	…
  y=ax2+bx+c	…	t	m	-2	-2	n	…

  且當x=-

  1

  2

  時，與其對應的函數值y＞0．有下列結論：
  ①abc＞0；②-2和3是關于x的方程ax²+bx+c=t的兩個根；③0＜m+n＜

  20

  3

  ．
  其中，正確結論的個數是（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：4652引用：20難度：0.6

  解析

• 6．如圖，將一個小球從斜坡的點O處拋出，小球的拋出路線可以用二次函數y=4x-

  1

  2

  x²刻畫，斜坡可以用一次函數y=

  1

  2

  x刻畫，下列結論錯誤的是（　　）

  A．當小球拋出高度達到7.5m時，小球距O點水平距離為3m

  B．小球距O點水平距離超過4米呈下降趨勢

  C．小球落地點距O點水平距離為7米

  D．斜坡的坡度為1：2
  組卷：1265引用：15難度：0.7

  解析

• 7．關于x 的一元二次方程

  a

  x

  2

  +

  bx

  +

  1

  2

  =

  0

  有一個根是-1，若二次函數

  y

  =

  a

  x

  2

  +

  bx

  +

  1

  2

  的圖象的頂點在第一象限，設t=2a+b,則t的取值范圍是（　　）

  A． - 1 2 ＜ t ＜ 1 4

  B． - 1 ＜ t ≤ 1 4

  C． - 1 2 ≤ t ＜ 1 2

  D． - 1 ＜ t ＜ 1 2
  組卷：85引用：2難度：0.4

  解析

三、解答題（本大題共8小題，共55分。解答應寫出文字說明，證明過程或演算步驟）

• 22．如圖1，在Rt△ABC中，∠A=90°，AB=6，sinB=

  4

  5

  ．點D為AB的中點，過點D作射線DE∥BC交AC于點E，點M為射線DE上一動點，過點M作MN⊥BC于點N，點P為邊AC上一點，連結NP，且滿足

  AP

  BN

  =

  4

  5

  ，設BN=x,NP=y.
  （1）求線段MN的長；
  （2）求y關于x的函數表達式；
  （3）如圖2，連結MP．
  ①當△MNP為等腰三角形時，求x的值．
  ②以點M為旋轉中心，將線段MP按順時針方向旋轉90°得線段MP′，當點P′落在BC邊上時，求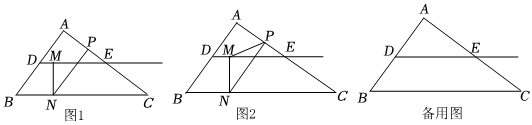

  NP

  AB

  的值．
  
  組卷：571引用：6難度：0.1

  解析

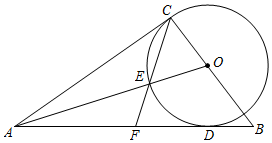• 23．如圖，在△ABC的邊BC上取一點O，以O為圓心，OC為半徑畫⊙O，⊙O與邊AB相切于點D，AC=AD，連接OA交⊙O于點E，連接CE，并延長交線段AB于點F．
  （1）求證：AC是⊙O的切線；
  （2）若AB=10，tanB=

  4

  3

  ，求⊙O的半徑；
  （3）若F是AB的中點，試探究BD+CE與AF的數量關系并說明理由．
  組卷：6100引用：25難度：0.2

  解析