2013-2014學年廣東省仲元中學、中山一中、南海桂城中學等七校聯考高二（下）入學數學試卷（文科）

一、選擇題：（本大題共10小題，每小題5分，滿分50分）

• 1．已知集合A={x|x＞1}，B={x|x²-2x＜0}，則A∩B=（　　）

  A．{x|x＞0}

  B．{x|x＞1}

  C．{x|1＜x＜2}

  D．{x|0＜x＜2}
  組卷：38引用：8難度：0.9

  解析

• 2．下列函數中，既是偶函數又在區間（0，+∞）上單調遞增的函數為（　　）

  A．y=x-1

  B．y=log2x

  C．y=|x|

  D．y=-x2
  組卷：43引用：22難度：0.9

  解析

• 3．公比為2的等比數列{a_n}的各項都是正數，且a₂a₁₂=16，則log₂a₉=（　　）

  A．4

  B．5

  C．6

  D．7
  組卷：39引用：4難度：0.9

  解析

• 4．“a=-1”是“直線a²x-y+6=0與直線4x-（a-3）y+9=0互相垂直”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：229引用：44難度：0.7

  解析

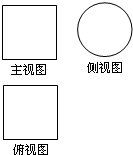• 5．如圖所示，一個空間幾何體的主視圖和俯視圖都是邊長為1的正方形，側視圖是一個直徑為1的圓，那么這個幾何體的表面積為（　　）

  A．4π

  B．3π

  C．2π

  D． 3 2 π
  組卷：23引用：7難度：0.9

  解析

• 6．在△ABC中，已知向量

  AB

  =

  （

  cos

  18

  °

  ，

  cos

  72

  °

  ）

  ，

  AC

  =

  （

  2

  cos

  63

  °

  ，

  2

  cos

  27

  °

  ）

  ，則cos∠BAC的值為（　　）

  A．0

  B． 1 2

  C． 2 2

  D． 3 2
  組卷：93引用：8難度：0.9

  解析

三、解答題（本大題共6小題，滿分80分）

• 19．已知函數y=f（x）的定義域為[-1，1]，且f（-x）=-f（x），f（1）=1，當a,b∈[-1，1]且a+b≠0，時

  f

  （

  a

  ）

  +

  f

  （

  b

  ）

  a

  +

  b

  ＞

  0

  恒成立．
  （1）判斷f（x）在[-1，1]上的單調性；
  （2）解不等式

  f

  （

  x

  +

  1

  2

  ）

  ＜

  f

  （

  1

  x

  -

  1

  ）

  ；
  （3）若f（x）＜m²-2am+1對于所有x∈[-1，1]，a∈[-1，1]恒成立，求m的取值范圍．
  組卷：156引用：9難度：0.1

  解析

• 20．設S_n為數列{a_n}的前n項和，對任意的n∈N^*，都有S_n=（m+1）-ma_n（m為常數，且m＞0）．
  （1）求證：數列{a_n}是等比數列．
  （2）設數列{a_n}的公比q=f（m），數列{b_n}滿足b₁=2a₁，b_n=f（b_n-1）（n≥2，n∈N^*），求數列{b_n}的通項公式．
  （3）在滿足（2）的條件下，求數列

  {

  2

  n

  +

  1

  b

  n

  }

  的前n項和T_n
  組卷：340引用：16難度：0.5

  解析