2022-2023學年山東省青島五十八中高一（下）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．復數z在復平面內對應的點為（2，1），則

  2

  i

  z

  -

  1

  =（　　）

  A．1+i

  B．1-i

  C．-1+i

  D．-1-i
  組卷：221引用：9難度：0.8

  解析

• 2．下列說法中正確的是（　　）

  A．直四棱柱是長方體

  B．圓柱的母線和它的軸可以不平行

  C．正棱錐的側面是全等的等腰三角形

  D．以直角三角形的一邊所在直線為旋轉軸，其余兩邊旋轉一周形成的面所圍成的旋轉體為圓錐
  組卷：181引用：4難度：0.8

  解析

• 3．已知向量

  AB

  =

  （

  9

  ，

  x

  ）

  ，

  CD

  =

  （

  x

  ,

  1

  ）

  ，若

  AB

  與

  CD

  同向共線，則x=（　　）

  A．3

  B．-3

  C．-3或3

  D．0或3
  組卷：474引用：6難度：0.8

  解析

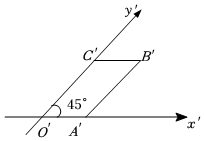• 4．如圖所示，一個水平放置的平面圖形OABC的斜二測直觀圖是平行四邊形O'A'B'C'，且OC'=2O'A'=2，∠A'O'C'=45°，則平面圖形OABC的周長為（　　）

  A．12

  B． 4 2

  C．5

  D．10
  組卷：167引用：5難度：0.8

  解析

• 5．已知

  e

  1

  ，

  e

  2

  是不共線的非零向量，則以下向量可以作為基底的是（　　）

  A． a = 0 ， b = e 1 - e 2	B． a = 3 e 1 - 3 e 2 ， b = e 1 - e 2
  C． a = e 1 - 2 e 2 ， b = e 1 + 2 e 2	D． a = e 1 - 2 e 2 ， b = 2 e 1 - 4 e 2
  組卷：141引用：7難度：0.8

  解析

• 6．將函數f（x）=sinx-cosx的圖象向左平移

  7

  π

  12

  個單位長度，得到函數y=g（x）的圖象，關于函數y=g（x）的下列說法中錯誤的是（　　）

  A．周期是2π

  B．非奇非偶函數

  C．圖象關于點 （ 5 π 3 ， 0 ） 中心對稱

  D．在 （ 0 ， π 2 ） 內單調遞增
  組卷：212引用：3難度：0.6

  解析

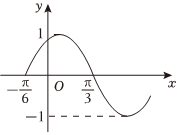• 7．已知函數f（x）=sin（ωx+φ）（ω＞0，0≤φ≤π）的部分圖像如圖所示，則

  f

  （

  11

  π

  24

  ）

  =（　　）

  A． 2 2

  B． - 2 2

  C． - 3 2

  D． - 1 2
  組卷：37引用：6難度：0.7

  解析

四、解答題本本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．閱讀材料：三角形的重心、垂心、內心和外心是與三角形有關的四個特殊點，它們與三角形的頂點或邊都具有一些特殊的性質．
  （一）三角形的“四心”
  1．三角形的重心：三角形三條中線的交點叫做三角形的重心，重心到頂點的距離與重心到對邊中點的距離之比為2：1．
  2．三角形的垂心：三角形三邊上的高的交點叫做三角形的垂心，垂心和頂點的連線與對邊垂直．
  3．三角形的內心：三角形三條內角平分線的交點叫做三角形的內心，也就是內切圓的圓心，三角形的內心到三邊的距離相等，都等于內切圓半徑r.
  4三角形的外心：三角形三條邊的垂直平分線的交點叫做三角形的外心，也就是三角形外接圓的圓心，它到三角形三個頂點的距離相等．
  （二）三角形“四心”的向量表示
  在△ABC中，角A，B，C所對的邊分別為a,b,c.
  1．三角形的重心：

  OA

  +

  OB

  +

  OC

  =

  0

  ?

  O

  是△ABC的重心．
  2．三角形的垂心：

  OA

  ?

  OB

  =

  OB

  ?

  OC

  =

  OC

  ?

  OA

  ?

  O

  是△ABC的垂心．
  3．三角形的內心：

  a

  OA

  +

  b

  OB

  +

  c

  OC

  =

  0

  ?

  O

  是△ABC的內心．
  4．三角形的外心：

  |

  OA

  |

  =

  |

  OB

  |

  =

  |

  OC

  |

  ?

  O

  是△ABC的外心．
  研究三角形“四心”的向量表示，我們就可以把與三角形“四心”有關的問題轉化為向量問題，充分利用平面向量的相關知識解決三角形的問題，這在一定程度上發揮了平面向量的工具作用，也很好地體現了數形結合的數學思想．
  結合閱讀材料回答下面的問題：
  （1）在△ABC中，若A（1，1），B（3，5），C（2，6），求△ABC的重心G的坐標；
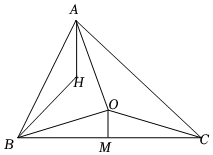
  （2）如圖所示，在非等腰的銳角△ABC中，已知點H是△ABC的垂心，點O是△ABC的外心．若M是BC的中點，求證：OM∥AH且OM=

  1

  2

  AH．
  組卷：335引用：2難度：0.5

  解析

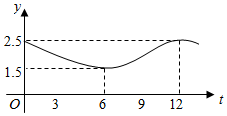• 22．某企業一天中不同時刻的用電量y（萬千瓦時）關于時間t（小時，0≤t≤24）的函數y=f（t）近似滿足f（t）=Asin（ωt+φ）+B，（A＞0，ω＞0，0＜φ＜π）．如圖是函數y=f（t）的部分圖象（t=0對應凌晨0點）．
  （Ⅰ）根據圖象，求A，ω，φ，B的值；
  （Ⅱ）由于當地冬季霧霾嚴重，從環保的角度，既要控制火力發電廠的排放量，電力供應有限；又要控制企業的排放量，于是需要對各企業實行分時拉閘限電措施．已知該企業某日前半日能分配到的供電量g（t）（萬千瓦時）與時間t（小時）的關系可用線性函數模型g（t）=-2t+25（0≤t≤12）模擬．當供電量小于該企業的用電量時，企業就必須停產．初步預計停產時間在中午11點到12點間，為保證該企業既可提前準備應對停產，又可盡量減少停產時間，請從這個初步預計的時間段開始，用二分法幫其估算出精確到15分鐘的停產時間段．
  組卷：195引用：4難度：0.5

  解析