人教版必修4《第一章 三角函數》2020年單元測試卷（二）

一、選擇題（本大題共12個小題，每小題5分，共60分，在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．sin600°的值為（　　）

  A．- 3 2

  B． 3 2

  C．- 1 2

  D． 1 2
  組卷：737引用：189難度：0.7

  解析

• 2．若sinx?cosx＜0，則角x的終邊位于（　　）

  A．第一、二象限	B．第二、三象限
  C．第二、四象限	D．第三、四象限
  組卷：492引用：9難度：0.7

  解析

• 3．函數y=tan

  x

  2

  是（　　）

  A．周期為π的奇函數	B．周期為 π 2 的奇函數
  C．周期為2π的奇函數	D．周期為2π的偶函數
  組卷：316引用：9難度：0.9

  解析

• 4．已知tan（-α-

  4

  3

  π）=-5，則tan（

  π

  3

  +α）的值為（　　）

  A．5

  B．-5

  C．±5

  D．不確定
  組卷：281引用：5難度：0.9

  解析

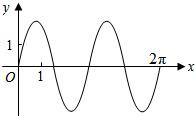• 5．已知函數y=2sin（ωx+φ）（ω＞0）在區間[0，2π]的圖象如圖：那么ω=（　　）

  A．1

  B．2

  C． 1 2

  D． 1 3
  組卷：889引用：16難度：0.9

  解析

• 6．函數f（x）=cos（3x+φ）的圖象關于原點成中心對稱，則φ等于（　　）

  A．- π 2	B．2kπ- π 2 （k∈Z）
  C．kπ（k∈Z）	D．kπ+ π 2 （k∈Z）
  組卷：827引用：4難度：0.9

  解析

• 7．若

  sinθ

  +

  cosθ

  sinθ

  -

  cosθ

  =2，則sinθ?cosθ=（　　）

  A． - 3 10

  B． 3 10

  C． ± 3 10

  D． 3 4
  組卷：597引用：14難度：0.9

  解析

三、解答題（本大題共6個小題，共70分，解答應寫出文字說明，證明過程或演算步驟）

• 21．函數y=Asin（ωx+φ）（A＞0，ω＞0，0≤φ≤

  π

  2

  ）在x∈（0，7π）內只取到一個最大值和一個最小值，且當x=π時，y_max=3；當x=6π，y_min=-3．
  （1）求出此函數的解析式；
  （2）求該函數的單調遞增區間；
  （3）是否存在實數m,滿足不等式Asin（ω

  -

  m

  2

  +

  2

  m

  +

  3

  +φ）＞Asin（ω

  -

  m

  2

  +

  4

  +φ）？若存在，求出m的范圍（或值），若不存在，請說明理由．
  組卷：165引用：7難度：0.5

  解析

• 22．已知某海濱浴場的海浪高度y（m）是時間t（0≤t≤24，單位：h）的函數，記作y=f（t），如表是某日各時的浪高數據：
  

  t/時	0	3	6	9	12	15	18	21	24
  y/米	1.5	1.0	0.5	1.0	1.5	1.0	0.5	0.99	1.5

  經長期觀測，y=f（t）的曲線可近似地看成是函數y=Acosωt+b.
  （1）求函數y=Acosωt+b的最小正周期T，振幅A及函數表達式．
  （2）依據規定：當海浪高度高于1m時才對沖浪愛好者開放，請依據（1）的結論，一天內的上午8：00時至晚上20：00時之間，有多少時間可供沖浪者進行運動．
  組卷：120引用：16難度：0.5

  解析