2022-2023學年江蘇省泰州中學高一(上)期中數學試卷
發(fā)布:2024/12/8 3:30:2
一、單選題(共8題,每題5分)
-
1.已知集合M滿足{1,2}?M?{1,2,3,4,5},這樣的集合M有( )個.
A.7 B.8 C.9 D.10 組卷:1516引用:16難度:0.9 -
2.命題“?x0∈(0,+∞),lnx0=x0-1”的否定是( )
A.?x0∈(0,+∞),lnx0≠x0-1 B.?x0?(0,+∞),lnx0=x0-1 C.?x∈(0,+∞),lnx≠x-1 D.?x?(0,+∞),lnx=x-1 組卷:4907引用:126難度:0.9 -
3.設α∈
,則使函數y=xα的定義域為R且為奇函數的所有α的值為( ){-1,1,12,3}A.-1,1,3 B. ,112C.-1,3 D.1,3 組卷:836引用:19難度:0.9 -
4.已知x>0,y>0,且x+y=2,則
的最小值為( )1x+9yA.8 B.6 C.4 D.2 組卷:252引用:6難度:0.7 -
5.若函數y=f(x)的定義域為M={x|-2≤x≤2},值域為N={y|0≤y≤2},則函數y=f(x)的圖象可能是( )
A. 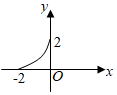
B. 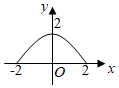
C. 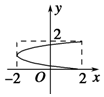
D. 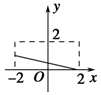 組卷:7252引用:82難度:0.9
組卷:7252引用:82難度:0.9 -
6.已知函數f(x)=
是R上的遞減函數,則實數a的取值范圍是( )1x,(x≤-1)ax2+4ax+1+4a,(x>-1)A. a≤-23B. a≤-38C.a≤-2 D.a≤-1 組卷:299引用:5難度:0.7 -
7.若f(x)是奇函數,且在(0,+∞)上是增函數,又f(-3)=0,則x2f(x)<0的解是( )
A.(-3,0)∪(1,+∞) B.(-∞,-3)∪(0,3) C.(-∞,-3)∪(3,+∞) D.(-3,0)∪(1,3) 組卷:51引用:2難度:0.7
四、解答題
-
21.已知y=f(x)是冪函數.
(1)若函數y=f(x)過定點,求函數y=f(x)的表達式和定義域;(4,12)
(2)若,求實數a的取值范圍.f(x)=x-32,f(a2+1)<f(a+3)組卷:155引用:3難度:0.7 -
22.已知函數f(x)是R上的偶函數,當x≥0時,f(x)=2x2+x.
(1)當x<0時,求f(x)解析式;
(2)若f(1-a)-f(2a+1)<0,求實數a的取值范圍.組卷:236引用:4難度:0.5


