人教A版高二（下）高考題單元試卷：第1章 三角函數（03）

一、選擇題（共12小題）

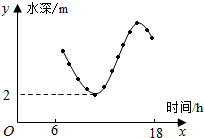• 1．如圖，某港口一天6時到18時的水深變化曲線近似滿足函數y=3sin（

  π

  6

  x+φ）+k.據此函數可知，這段時間水深（單位：m）的最大值為（　　）

  A．5

  B．6

  C．8

  D．10
  組卷：2604引用：35難度：0.9

  解析

• 2．設函數f（x）=cosωx（ω＞0），將y=f（x）的圖象向右平移

  π

  3

  個單位長度后，所得的圖象與原圖象重合，則ω的最小值等于（　　）

  A． 1 3

  B．3

  C．6

  D．9
  組卷：5791引用：76難度：0.9

  解析

• 3．若函數

  f

  （

  x

  ）

  =

  sin

  x

  +

  φ

  3

  （

  φ

  ∈

  [

  0

  ，

  2

  π

  ]

  ）

  是偶函數，則φ=（　　）

  A． π 2

  B． 2 π 3

  C． 3 π 2

  D． 5 π 3
  組卷：1770引用：47難度：0.9

  解析

• 4．函數y=sin（2x+φ）的圖象沿x軸向左平移

  π

  8

  個單位后，得到一個偶函數的圖象，則φ的一個可能的值為（　　）

  A． 3 π 4

  B． π 4

  C．0

  D． - π 4
  組卷：3002引用：115難度：0.9

  解析

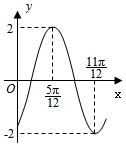• 5．函數f（x）=2sin（ωx+φ）（ω＞0，-

  π

  2

  ＜φ＜

  π

  2

  ）的部分圖象如圖所示，則ω，φ的值分別是（　　）

  A． 2 ，- π 3

  B． 2 ，- π 6

  C． 4 ，- π 6

  D． 4 ， π 3
  組卷：4445引用：114難度：0.9

  解析

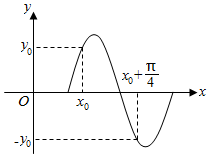• 6．若函數y=sin（ωx+φ）（ω＞0）的部分圖象如圖，則ω=（　　）

  A．5

  B．4

  C．3

  D．2
  組卷：2470引用：30難度：0.7

  解析

• 7．若將函數f（x）=sin2x+cos2x的圖象向右平移φ個單位，所得圖象關于y軸對稱，則φ的最小正值是（　　）

  A． π 8

  B． π 4

  C． 3 π 8

  D． 3 π 4
  組卷：3794引用：88難度：0.7

  解析

• 8．為了得到函數y=sin（2x-

  π

  3

  ）的圖象，只需把函數y=sin（2x+

  π

  6

  ）的圖象（　　）

  A．向左平移 π 4 個長度單位	B．向右平移 π 4 個長度單位
  C．向左平移 π 2 個長度單位	D．向右平移 π 2 個長度單位
  組卷：1880引用：104難度：0.9

  解析

• 9．將函數y=3sin（2x+

  π

  3

  ）的圖象向右平移

  π

  2

  個單位長度，所得圖象對應的函數（　　）

  A．在區間[ π 12 ， 7 π 12 ]上單調遞增

  B．在區間[ π 12 ， 7 π 12 ]上單調遞減

  C．在區間[- π 6 ， π 3 ]上單調遞減

  D．在區間[- π 6 ， π 3 ]上單調遞增
  組卷：3987引用：78難度：0.9

  解析

• 10．將函數f（x）=sin（2x+θ）（

  -

  π

  2

  ＜

  θ

  ＜

  π

  2

  ）的圖象向右平移φ（φ＞0）個單位長度后得到函數g（x）的圖象，若f（x），g（x）的圖象都經過點P（

  0

  ，

  3

  2

  ），則φ的值可以是（　　）

  A． 5 π 3

  B． 5 π 6

  C． π 2

  D． π 6
  組卷：1377引用：34難度：0.7

  解析

三、解答題（共8小題）

• 29．已知函數f（x）=10

  3

  sin

  x

  2

  cos

  x

  2

  +10cos²

  x

  2

  ．
  （Ⅰ）求函數f（x）的最小正周期；
  （Ⅱ）將函數f（x）的圖象向右平移

  π

  6

  個單位長度，再向下平移a（a＞0）個單位長度后得到函數g（x）的圖象，且函數g（x）的 最大值為2．
  （ⅰ）求函數g（x）的解析式；
  （ⅱ）證明：存在無窮多個互不相同的正整數x₀，使得g（x₀）＞0．
  組卷：2563引用：14難度：0.3

  解析

• 30．已知函數f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的周期為π，圖象的一個對稱中心為（

  π

  4

  ，0），將函數f（x）圖象上所有點的橫坐標伸長到原來的2倍（縱坐標不變），再將得到的圖象向右平移個

  π

  2

  單位長度后得到函數g（x）的圖象．
  （1）求函數f（x）與g（x）的解析式
  （2）是否存在x₀∈（

  π

  6

  ，

  π

  4

  ），使得f（x₀），g（x₀），f（x₀）g（x₀）按照某種順序成等差數列？若存在，請確定x₀的個數，若不存在，說明理由；
  （3）求實數a與正整數n,使得F（x）=f（x）+ag（x）在（0，nπ）內恰有2013個零點．
  組卷：3455引用：11難度：0.1

  解析