2023-2024學(xué)年黑龍江省哈爾濱師大附中高一（上）期中數(shù)學(xué)試卷

一、選擇題（本大題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)符合題目要求的）

• 1．命題“?x＞0，lnx≤x+1”的否定是（　　）

  A．?x＞0，lnx＞x+1	B．?x＞0，lnx＞x+1
  C．?x≤0，lnx＞x+1	D．?x≤0，lnx＞x+1
  組卷：13引用：1難度：0.8

  解析

• 2．已知集合A={x||x-2|≤1}，B={x|e^x-1≥1}，則A∪（?_RB）=（　　）

  A．（-1，3]

  B．[-1，3]

  C．（-∞，3）

  D．（-∞，3]
  組卷：15引用：1難度：0.9

  解析

• 3．已知函數(shù)y=f（x+1）定義域是[0，1]，則

  y

  =

  f

  （

  2

  x

  -

  1

  ）

  的定義域是（　　）

  A．[0，1]

  B．[1，2]

  C． [ 1 ， 5 2 ]

  D．[2，5]
  組卷：91引用：1難度：0.8

  解析

• 4．通過加強(qiáng)對(duì)野生動(dòng)物的棲息地保護(hù)和拯救繁育，某瀕危野生動(dòng)物的數(shù)量不斷增長(zhǎng)，根據(jù)調(diào)查研究，該野生動(dòng)物的數(shù)量

  N

  （

  t

  ）

  =

  K

  1

  +

  e

  -

  0

  .

  12

  t

  -

  0

  .

  8

  （t的單位：年），其中K為棲息地所能承受該野生動(dòng)物的最大數(shù)量．當(dāng)N（t^*）=0.8K時(shí)，該野生動(dòng)物的瀕危程度降到較為安全的級(jí)別，此時(shí)t^*約為（ln2≈0.70）（　　）

  A．7

  B．6

  C．5

  D．4
  組卷：37引用：2難度：0.6

  解析

• 5．設(shè)函數(shù)

  f

  （

  x

  ）

  =

  2

  f

  （

  1

  x

  ）

  ?

  lgx

  +

  1

  ，則f（10）等于（　　）

  A． 3 5

  B．1

  C．-1

  D．10
  組卷：163引用：2難度：0.7

  解析

• 6．函數(shù)f（x）=ln|x+1|的圖象大致是（　　）

  A．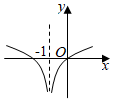

  B．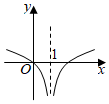

  C．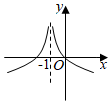

  D．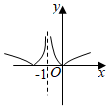
  組卷：148引用：4難度：0.8

  解析

• 7．函數(shù)

  f

  （

  x

  ）

  =

  lo

  g

  a

  （

  x

  2

  -

  ax

  +

  1

  ）

  在[2，+∞）單調(diào)遞增，則實(shí)數(shù)a的取值范圍（　　）

  A．0＜a＜1

  B．1＜a≤2

  C． 1 ＜ a ＜ 5 2

  D．1＜a≤4
  組卷：601引用：1難度：0.7

  解析

四、解答題（本大題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.）

• 21．已知函數(shù)f（x）=2^x-2^-x．
  （Ⅰ）判斷函數(shù)f（x）在（-∞，+∞）上的單調(diào)性，并利用單調(diào)性定義進(jìn)行證明；
  （Ⅱ）函數(shù)g（x）=x²-4x+6，若對(duì)任意的x₁∈[1，4]，總存在x₂∈[0，2]，使得g（x₁）=mf（x₂）+7-3m成立，求實(shí)數(shù)m的取值范圍．
  組卷：40引用：4難度：0.4

  解析

• 22．已知函數(shù)f（x）=log_m（x-m）+log_m（x-2m）（m＞0且m≠1）．
  （Ⅰ）當(dāng)m=2時(shí)，解不等式f（x）＜log₂3；
  （Ⅱ）若對(duì)任意的x∈[3m,4m]，都有f（x）≤1，求實(shí)數(shù)m的取值范圍；
  （Ⅲ）在（Ⅱ）的條件下，是否存在

  α

  ，

  β

  ∈

  （

  5

  2

  m

  ,

  +

  ∞

  ）

  ，使得f（x）在區(qū)間[α，β]上的值域是[log_mβ，log_mα]，若存在，求實(shí)數(shù)m的取值范圍；若不存在，說明理由．
  組卷：223引用：1難度：0.4

  解析