2022-2023學年江蘇省蘇州市常熟中學高二（下）調研數(shù)學試卷（5月份）

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．若隨機變量X服從正態(tài)分布N（3，σ²），且P（X≤4）=0.64，則P（2≤X≤3）=（　　）

  A．0.07

  B．0.14

  C．0.28

  D．0.36
  組卷：33引用：2難度：0.7

  解析

• 2．已知集合

  A

  =

  {

  x

  |

  y

  =

  1

  x

  }

  ，

  B

  =

  {

  y

  |

  y

  =

  ln

  1

  -

  x

  }

  ，則A∩B=（　　）

  A．?	B．（0，+∞）
  C．（0，1）	D．（-∞，0）∪（0，+∞）
  組卷：33引用：2難度：0.7

  解析

• 3．已知a,b∈R，則使得“a＞b＞0”成立的一個充分不必要條件為（　　）

  A． 1 a ＞ 1 b

  B．a(chǎn)3＞b3

  C． a - 1 ＞ b - 1

  D．lna＞lnb
  組卷：49引用：2難度：0.7

  解析

• 4．“學如逆水行舟，不進則退；心似平原跑馬，易放難收”（明?《增廣賢文》）是勉勵人們專心學習的．如果每天的“進步”率都是1%，那么一年后是（1+1%）³⁶⁵=1.01³⁶⁵；如果每天的“退步”率都是1%，那么一年后是（1-1%）³⁶⁵=0.99³⁶⁵.一年后“進步”的是“退步”的

  1

  .

  01

  365

  0

  .

  99

  365

  =

  （

  1

  .

  01

  0

  .

  99

  ）

  365

  ≈

  1481

  倍．如果每月的“進步”率和“退步”率都是20%，那么大約經(jīng)過（　　）月后“進步”的是“退步”的一萬倍．（lg2≈0.3010，lg3≈0.4771）

  A．20

  B．21

  C．22

  D．23
  組卷：309引用：9難度：0.8

  解析

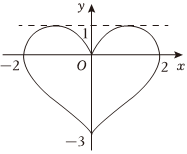• 5．如圖所示的“心形”圖形可看作由兩個函數(shù)的圖象構成，則“心形”圖形在x軸上方的圖象對應的函數(shù)解析式可能為（　　）

  A． y = - x 2 + 2 | x |

  B． y = x 4 - x 2

  C． y = | x | 4 - x 2

  D． y = - x 2 + 2 x
  組卷：129引用：3難度：0.6

  解析

• 6．已知函數(shù)f（x-1）為偶函數(shù)，且函數(shù)f（x）在[-1，+∞）上單調遞增，則關于x的不等式f（1-2^x）＜f（-7）的解集為（　　）

  A．（-∞，3）

  B．（3，+∞）

  C．（-∞，2）

  D．（2，+∞）
  組卷：218引用：6難度：0.6

  解析

• 7．若（mx-1）ⁿ（n∈N^*）的展開式中，所有項的系數(shù)和與二項式系數(shù)和相等，且第6項的二項式系數(shù)最大，則有序實數(shù)對（m,n）共有（　　）組不同的解．

  A．1

  B．2

  C．3

  D．4
  組卷：239引用：7難度：0.8

  解析

四、解答題：本大題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟.

• 21．甲、乙，丙三位學徒跟師傅學習制作某種陶器，經(jīng)過一段時間的學習后，他們各自能制作成功該陶器的概率分別為p₁，p₂，p₃，且0＜p₃＜p₂＜p₁＜1，現(xiàn)需要他們三人制作一件該陶器，每次只有一個人制作且每個人只制作一次，如果有一個人制作失敗則換下一個人重新制作，若陶器制作成功則結束．
  （1）按甲、乙、丙的順序制作陶器，若

  p

  1

  p

  2

  =

  2

  9

  ，

  p

  1

  ∈

  [

  2

  3

  ，

  1

  ）

  ，求制作陶器人數(shù)X的數(shù)學期望的最大值．
  （2）若這種陶器制作成功后需要檢測合格才能上市銷售，如果這種陶器可以上市銷售，則每件陶器可獲利100元；如果這種陶器不能上市銷售，則每件陶器虧損80元，已知甲已經(jīng)制成了4件這種陶器，且甲制作的陶器檢測合格的概率為

  2

  5

  ，求這4件陶器最終盈虧Y的概率分布和數(shù)學期望．
  組卷：37引用：4難度：0.5

  解析

• 22．已知函數(shù)f（x）=axe^x-ln（x+1）（a∈R）．
  （1）討論f（x）的極值點的個數(shù)；
  （2）若f（x）≥2lna-3ln2-3恒成立，求實數(shù)a的最大值．
  組卷：41引用：2難度：0.3

  解析