2022-2023學(xué)年天津市寧河區(qū)蘆臺一中高二（上）期末數(shù)學(xué)試卷

一、選擇題（每小題5分，共45分）

• 1．橢圓

  x

  2

  25

  +

  y

  2

  9

  =

  1

  上一點(diǎn)P到一個焦點(diǎn)的距離為7，則P點(diǎn)到另一個焦點(diǎn)的距離為（　　）

  A．5

  B．3

  C．4

  D．7
  組卷：337引用：1難度：0.8

  解析

• 2．已知等差數(shù)列{a_n}滿足a₅+a₆=18，則其前10項(xiàng)之和為（　　）

  A．90

  B．180

  C．99

  D．81
  組卷：608引用：1難度：0.8

  解析

• 3．雙曲線

  y

  2

  4

  -

  x

  2

  =

  1

  的漸近線方程是（　　）

  A． x ± 2 y = 0

  B． 2 x ± y = 0

  C．x±2y=0

  D．2x±y=0
  組卷：261引用：2難度：0.8

  解析

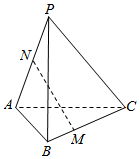• 4．如圖，在三棱錐P-ABC中，點(diǎn)N為棱AP的中點(diǎn)，點(diǎn)M在棱BC上，且滿足CM=2BM，設(shè)

  PA

  =

  a

  ，

  PB

  =

  b

  ，

  PC

  =

  c

  ，則

  MN

  =（　　）

  A．- 1 2 a + 2 3 b - 1 3 c	B． 1 2 a - 2 3 b - 1 3 c
  C． 1 2 a + 2 3 b - 1 3 c	D．- 1 2 a - 2 3 b + 1 3 c
  組卷：643引用：11難度：0.7

  解析

• 5．設(shè)a∈R，則“a=-2”是“直線l₁：ax+2y-1=0與直線l₂：x+（a+1）y+2=0平行”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：135引用：4難度：0.9

  解析

• 6．記等比數(shù)列{a_n}的前n項(xiàng)和為S_n，若S₄=3，S₈=9，則S₁₂=（　　）

  A．12

  B．18

  C．21

  D．27
  組卷：1101引用：14難度：0.6

  解析

三、解答題（本大題共5小題，共75分．解答應(yīng)寫出必要的文字說明、證明過程或演算步驟，請把解題過程寫在答案紙上．）

• 19．已知點(diǎn)F為橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的右焦點(diǎn)，A為橢圓的左頂點(diǎn)，橢圓的離心率為

  3

  2

  ，連接橢圓的四個頂點(diǎn)得到的菱形的面積為4．
  （1）求橢圓的方程；
  （2）設(shè)過點(diǎn)A作斜率為k的直線交橢圓于另一點(diǎn)B，
  ①求

  FA

  ?

  FB

  的取值范圍；
  ②若

  |

  AB

  |

  =

  4

  3

  9

  ，求k的值．
  組卷：268引用：1難度：0.6

  解析

• 20．已知數(shù)列{a_n}和數(shù)列{b_n}，滿足nb_n+1-（n+1）b_n=n（n+1）（n∈N^*），且b₁=1，a_n=3

  b

  n

  n

  +1．
  （1）證明數(shù)列

  {

  b

  n

  n

  }

  為等差數(shù)列，并求{b_n}的通項(xiàng)公式；
  （2）證明：

  1

  a

  2

  1

  +

  1

  a

  2

  2

  +

  1

  a

  2

  3

  +

  ?

  +

  1

  a

  2

  n

  ＜

  1

  3

  -

  1

  9

  n

  +

  3

  （

  n

  ∈

  N

  *

  ）

  ．
  組卷：384引用：1難度：0.6

  解析