2023-2024學年廣西崇左市寧明一中、寧明實驗學校、寧明中學初中部九年級（上）月考數學試卷（10月份）

一、選擇題（共12小題，每小題3分，共36分.在每小題給出的四個選項中只有一項是符合要求的，用2B鉛筆把答題卡上對應題目的答案標號涂黑.）

• 1．下列y關于x的函數中，是二次函數的是（　　）

  A．y=（x+1）2-x2	B．y=3x+2
  C．y=x3-x2+1	D．y=-x2+2x
  組卷：63引用：1難度：0.7

  解析

• 2．拋物線y=2x²的對稱軸是直線（　　）

  A．y=0

  B．y=1

  C．x=0

  D．x=2
  組卷：476引用：5難度：0.8

  解析

• 3．關于二次函數y=-（x-3）²+2的最值，下列說法正確的是（　　）

  A．有最大值3

  B．有最小值3

  C．有最大值2

  D．有最小值2
  組卷：138引用：6難度：0.8

  解析

• 4．已知二次函數y=ax²+bx+c的x、y部分對應值如表：
  

  x	-1	0	1	2	3
  y	5	1	-1	-1	1

  則當x=4時，y的值為（　　）

  A．5

  B．3

  C．1.5

  D．無法確定
  組卷：110引用：1難度：0.8

  解析

• 5．已知拋物線y=（x-3）²+1，下列結論錯誤的是（　　）

  A．拋物線開口向上

  B．頂點坐標是（-3，1）

  C．當x＜3時，y隨x的增大而減小

  D．拋物線與x軸沒有交點
  組卷：67引用：1難度：0.5

  解析

• 6．二次函數y=ax²+bx-1（a≠0）的圖象經過點（1，1），則代數式1-a-b的值為（　　）

  A．-3

  B．-1

  C．2

  D．5
  組卷：1661引用：71難度：0.7

  解析

• 7．拋物線y=5x²與拋物線y=-5（x+1）²的相同點是（　　）

  A．都有最低點	B．對稱軸相同
  C．開口方向相同	D．頂點都在x軸上
  組卷：71引用：1難度：0.7

  解析

• 8．在平面直角坐標系中，拋物線y=（x+5）（x-3）經變換后得到拋物線y=（x+3）（x-5），則這個變換可以是（　　）

  A．向左平移8個單位	B．向右平移8個單位
  C．向左平移2個單位	D．向右平移2個單位
  組卷：409引用：5難度：0.7

  解析

三、解答題（本大題共8小題，共72分。解答應寫出文字說明、證明過程或演算步驟）

• 25．如圖，拋物線y=ax²+bx+2與x軸交于點A（1，0）和B（4，0）．
  （1）求拋物線的解析式；
  （2）若拋物線的對稱軸交x軸于點E，點F是位于x軸上方的拋物線對稱軸上一點，C是第一象限拋物線上一點，若EF=2，點C的橫坐標是5，求證：四邊形OECF是平行四邊形；
  （3）在（2）的條件下，若點P是x軸上的一個動點，當△OCP是等腰三角形時，求點P的坐標．
  組卷：70引用：1難度：0.5

  解析

• 26．【定義】若拋物線與一水平直線交于兩點，我們把這兩點間線段的長稱為拋物線關于這條直線的跨徑，拋物線的頂點到該直線的距離稱為拋物線關于這條直線的矢高，矢高與跨徑的比值稱為拋物線關于這條直線的矢跨比．
  如圖1，拋物線y=ax²+bx+c的頂點為P，PC⊥x軸于點C，它與x軸交于點A，B，則AB的長為拋物線y=ax²+bx+c關于x軸的跨徑，PC的長為拋物線y=ax²+bx+c關于x軸的矢高，

  PC

  AB

  的值為拋物線y=ax²+bx+c關于x軸的矢跨比．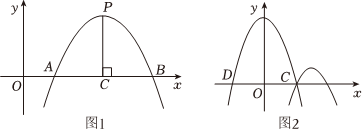
  
  【特例】如圖2，已知拋物線y=-x²+4與x軸交于點C，D（點C在點D右側）；
  ①拋物線y=-x²+4關于x軸的矢高是

  ，跨徑是

  ，矢跨比是

  ；
  ②有一拋物線經過點C，與拋物線y=-x²+4開口方向與大小一樣，且矢高是拋物線y=-x²+4關于x軸的矢高的

  1

  4

  ，求它關于x軸的矢跨比；
  【推廣】結合拋物線的平移規律可以發現，兩條開口方向與大小一樣的拋物線，若第一條拋物線的矢高是第二條拋物線關于同一直線的矢高的k（k＞0）倍，則第一條拋物線的跨徑是第二條拋物線關于同一直線的跨徑的

  倍（用含k的代數式表示）；
  【應用】如圖3是某地一座三拱橋梁建筑示意圖，其中主跨與邊跨的拱軸線為開口方向與大小一樣的拋物線，它們關于水平鋼梁所在直線的跨徑分別為420米與280米，已知主跨的矢跨比為

  1

  6

  ，則邊跨的矢跨比是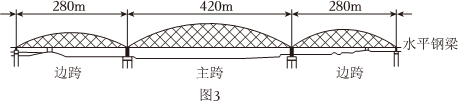

  ．
  
  組卷：1218引用：3難度：0.4

  解析