2022-2023學年江蘇省常州市武進區(qū)高一（下）期末數(shù)學試卷

一、選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．若復數(shù)z是x²+x+2=0的根，則|z|=（　　）

  A．1

  B． 2

  C．2

  D．3
  組卷：55引用：5難度：0.8

  解析

• 2．一個三角形的三條高的長度分別是

  1

  6

  ，

  1

  10

  ，

  1

  14

  ，則該三角形（　　）

  A．一定是銳角三角形

  B．一定是直角三角形

  C．一定是鈍角三角形

  D．有可能是銳角三角形，也可能是鈍角三角形
  組卷：35引用：4難度：0.8

  解析

• 3．已知l,m,n表示不同的直線，α，β，γ表示不同的平面，則下列四個命題正確的是（　　）

  A．若l∥α，且m∥α，則l⊥m	B．若α⊥β，m∥α，n⊥β，則m∥n
  C．若m∥l,且m⊥α，則l⊥α	D．若m⊥n,m⊥α，n∥β，則α⊥β
  組卷：73引用：4難度：0.5

  解析

• 4．已知

  cos

  （

  α

  -

  π

  6

  ）

  =

  1

  3

  ，則

  sin

  （

  2

  α

  +

  π

  6

  ）

  =（　　）

  A． - 7 9

  B． 7 9

  C． - 2 2 3

  D． 2 2 3
  組卷：409引用：10難度：0.7

  解析

• 5．疫情期間，一同學通過網(wǎng)絡平臺聽網(wǎng)課，在家堅持學習．某天上午安排了四節(jié)網(wǎng)課，分別是數(shù)學，語文，政治，地理，下午安排了三節(jié)，分別是英語，歷史，體育．現(xiàn)在，他準備在上午下午的課程中各任選一節(jié)進行打卡，則選中的兩節(jié)課中至少有一節(jié)文綜學科（政治、歷史、地理）課程的概率為（　　）

  A． 3 4

  B． 7 12

  C． 2 3

  D． 5 6
  組卷：207引用：7難度：0.7

  解析

• 6．已知z₁，z₂∈C，|z₁|=|z₂|=1，|z₁+z₂|=

  3

  ，則|z₁-z₂|=（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：122引用：5難度：0.7

  解析

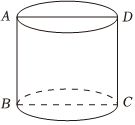• 7．如圖，某圓柱體的高為2，ABCD是該圓柱體的軸截面．已知從點B出發(fā)沿著圓柱體的側(cè)面到點D的路徑中，最短路徑的長度為

  2

  5

  ，則該圓柱體的體積是（　　）

  A．3

  B． 4 π

  C．32π

  D． 32 π
  組卷：103引用：3難度：0.8

  解析

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟.

• 21．甲、乙、丙三個學校進行籃球比賽，各出一個代表隊，簡稱甲隊、乙隊、丙隊．約定賽制如下：累計負兩場者被淘汰；比賽前抽簽決定首先比賽的兩個隊，另一隊輪空；每場比賽的勝隊與輪空隊進行下一場比賽，負隊下一場輪空，直至有一隊被淘汰；當一隊被淘汰后，剩余的兩隊繼續(xù)比賽，直至其中一隊被淘汰，另一隊最終獲勝，比賽結(jié)束．已知在每場比賽中，甲隊勝乙隊和甲隊勝丙隊的概率均為

  2

  3

  ，乙隊勝丙隊的概率為

  1

  2

  ，各場比賽的結(jié)果相互獨立．經(jīng)抽簽，第一場比賽甲隊輪空．
  （1）求“前三場比賽結(jié)束后，乙隊被淘汰”的概率；
  （2）求“一共只需四場比賽甲隊就獲得冠軍”的概率；
  （3）求“需要進行第五場比賽”的概率．
  組卷：180引用：3難度：0.7

  解析

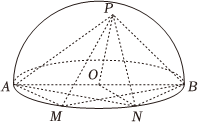• 22．如圖，AB是半球的直徑，O為球心，AB=4，M，N依次是半圓上的兩個三等分點，P是半球面上一點，且PN⊥MB．
  （1）證明：平面PBM⊥平面PON；
  （2）若點P在底面圓內(nèi)的射影恰在BM上，求點M到平面PAB的距離．
  組卷：92引用：3難度：0.4

  解析