當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省鹽城中學南北校區九年級（下）開學數學試卷

發布：2024/4/20 14:35:0

一、選擇題

1．下列函數中是二次函數的是（　　）
A．y=3x-1 B．y=3x²-1 C．y=
2
x
D．y=x³+2x-3
組卷：201引用：5難度：0.9
解析
2．若
x
y
=
5
3
，則
x
+
y
x
的值為（　　）
A．
2
5
B．
8
5
C．
2
3
D．
8
3
組卷：388引用：6難度：0.7
解析
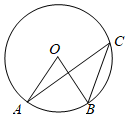3．如圖，A，B，C是⊙O上的三點，若∠O=70°，則∠C的度數是（　　）
A．40° B．35° C．30° D．25°
組卷：2529引用：23難度：0.8
解析
4．已知sinα=
3
2
，那么銳角α的度數是（　　）
A．30° B．45° C．60° D．75°
組卷：472引用：3難度：0.8
解析
5．已知圓與直線有兩個公共點，且圓心到直線的距離為4，則該圓的半徑可能為（　　）
A．2 B．3 C．4 D．5
組卷：503引用：4難度：0.8
解析
6．已知，點P是線段AB的黃金分割點（AP＞PB），若線段AB=2cm,則線段AP的長是（　　）
A．
5
-
1
2
cm B．（
5
-
1
）cm C．（
3
-
5
）cm D．（
2
-
5
）cm
組卷：213引用：3難度：0.9
解析
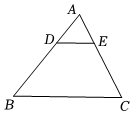7．如圖，在△ABC中，點D在邊AB上，BD=3AD，DE∥BC交AC于點E．若S_△ADE=1，則S_{四邊形BCED}為（　　）
A．15 B．3 C．16 D．4
組卷：381引用：4難度：0.9
解析
8．已知學校航模組設計制作的火箭的升空高度h（m）與飛行時間t（s）滿足函數表達式h=-t²+24t+1．則下列說法中正確的是（　　）
A．點火后9s和點火后13s的升空高度相同
B．點火后24s火箭落于地面
C．點火后10s的升空高度為139m
D．火箭升空的最大高度為145m
組卷：4584引用：46難度：0.7
解析

二、填空題

9．已知圓錐的底面半徑為3，母線長為7，則圓錐的側面積是
．
組卷：881引用：8難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題

26．【提出問題】小聰同學類比所學的“圓心角“與“圓周角”的概念，將頂點在圓內（頂點不在圓心）的角命名為圓內角．如圖1中，∠AEC，∠BED就是圓內角，所對的分別是
?
AC
、
?
BD
，那么圓內角的度數與所對弧的度數之間有什么關系呢？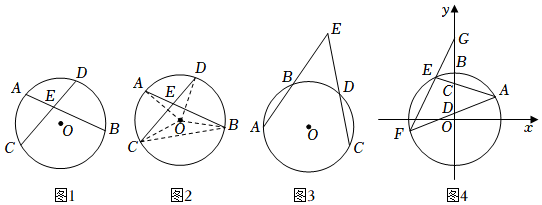

【解決問題】小聰想到了將圓內角轉化為學過的兩種角，即圓周角、圓心角，再進一步解決問題：

解：連接BC，OA，OC，OB，OD．
如圖2，在△BCE中，∠AEC=∠EBC+∠ECB
∵∠EBC=
1
2
∠AOC，∠ECB=
1
2
∠BOD
∴∠AEC=
1
2
∠AOC+
1
2
∠BOD=
1
2
（∠AOC+∠BOD）
即：∠AEC的度數=
1
2
（
?
AC
的度數+
?
BD
的度數）

（1）如圖1，在⊙O中，弦AB、CD相交于點E，若弧
?
AC
的度數是65°，弧
?
BD
的度數是40°，則∠AED的度數是
．
【類比探究】頂點在圓外且兩邊與圓相交的角，命名為圓外角．
（2）如圖3，在⊙O中，弦AB，CD的延長線相交于點E，試探索圓外角∠E的度數與它所夾的兩段弧
?
AC
、
?
BD
的度數之間的關系．
【靈活運用】
（3）如圖4，平面直角坐標系內，點A（
3
，1）在⊙O上，⊙O與y軸正半軸交于點B，點C，點D是線段OB上的兩個動點，滿足AC=AD．AC，AD的延長線分別交⊙O于點E、F．延長FE交y軸于點G，試探究∠FGO的度數是否變化．若不變，請求出它的度數；若變化，請說明理由．

組卷：240引用：1難度：0.4

解析

27．如圖1，二次函數y=ax²+bx+c的圖象交x軸于點A（-1，0），B（3，0），交y軸于點C（0，-3），直線l經過點B．
（1）求二次函數的表達式和頂點D的坐標；
（2）如圖2，當直線l過點D時，求△BCD的面積；
（3）如圖3，直線l與拋物線有另一個交點E，且點E使得∠BAC-∠CBE＞45°，求點E的橫坐標m的取值范圍；
（4）如圖4，動點F在直線l上，作∠CFG=45°，FG與線段AB交于點G，連接CG，當△ABC與△CFG相似，且S_△CFG最小時，在直線l上是否存在一點H，使得∠FHG=45°存在，請求出點H的坐標；若不存在，請說明理由．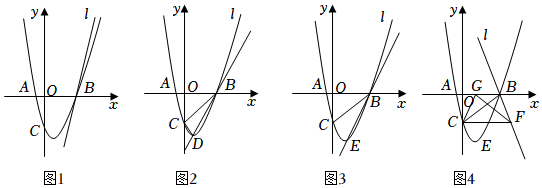
組卷：501引用：2難度：0.2
解析