當前位置：試卷中心 > 試卷詳情

2022-2023學年北京工業大學附中高一（下）期末數學試卷（二）

發布：2024/5/25 8:0:9

一、選擇題共10小題，每小題4分，共40分.在每小題列出的四個選項中，選出符合題目要求的一項.

1．復數z=1-2i的虛部為（　　）
A．1 B．i C．-2 D．-2i
組卷：154引用：7難度：0.8
解析
2．1，2，3，4，5，5這組數據的第50百分位數是（　　）
A．3 B．3.5 C．4 D．5
組卷：70引用：2難度：0.8
解析
3．在△ABC中，已知BC=6，AC=4，sinA=
3
4
，則角B=（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
組卷：311引用：2難度：0.7
解析
4．某班分成了A、B、C、D四個學習小組學習二十大報告，現從中隨機抽取兩個小組在班會課上進行學習成果展示，則A組和B組恰有一個組被抽到的概率為（　　）
A．
1
3
B．
1
2
C．
2
3
D．
5
6
組卷：441引用：4難度：0.8
解析
5．已知向量
a
=（2，1），
b
=（-1，k），若存在實數λ，使得
a
=λ
b
，則k和λ的值分別為（　　）
A．-
1
2
，-2 B．
1
2
，-2 C．-
1
2
，2 D．
1
2
，2
組卷：339引用：2難度：0.8
解析
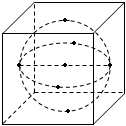6．如圖所示，該幾何體是從一個水平放置的正方體中挖去一個內切球（正方體各個面均與球面有且只有一個公共點）以后得到的，現用一豎直的平面去截這個幾何體，則截面圖形不可能是（　　）
A． B． C． D．
組卷：178引用：5難度：0.8
解析
7．已知直線a,b與平面α，β，γ，能使α∥β成立的條件是（　　）
A．α⊥γ，β⊥γ B．a∥α，a∥β
C．α∥γ，β∥γ D．a?α，b?α，a∥β，b∥β
組卷：139引用：3難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題共5小題，共70分.解答應寫出文字說明，演算步驟或證明過程.

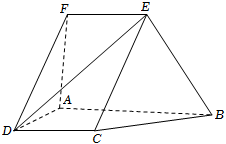20．如圖，在直角梯形ABCD中，AB∥CD，AB⊥AD，AB=2CD=2，并將直角梯形ABCD繞AB邊旋轉至ABEF．
（Ⅰ）求證：直線AB⊥平面ADF；
（Ⅱ）求證：直線CE∥平面ADF；
（Ⅲ）當平面ABCD⊥平面ABEF時，再從條件①、條件②、條件③這三個條件中選擇一個作為已知，使平面ADE與平面BCE垂直．并證明你的結論．
條件①：AE=
3
；
條件②：AD=1；
條件③：BE⊥DE．
注：如果選擇的條件不符合要求，第（Ⅲ）問得0分；如果選擇多個符合要求的條件分別解答，按第一個解答計分．
組卷：426引用：2難度：0.6
解析
21．在平面直角坐標系中，O為坐標原點，對任意兩個向量
m
=（x₁，y₁），
n
=（x₂，y₂），作：
OM
=
m
，
ON
=
n
．當
m
，
n
不共線時，記以OM，ON為鄰邊的平行四邊形的面積為S（
m
，
n
）=|x₁y₂-x₂y₁|；當
m
，
n
共線時，規定S（
m
，
n
）=0．
（Ⅰ）分別根據下列已知條件求S（
m
，
n
）：
①
m
=（2，1），
n
=（-1，2）；②
m
=（1，2），
n
=（2，4）；
（Ⅱ）若向量
p
=λ
m
+μ
n
（λ，μ∈R，λ²+μ²≠0），
求證：S（
p
，
m
）+S（
p
，
n
）=（|λ|+|μ|）S（
m
，
n
）；
（Ⅲ）若A，B，C是以O為圓心的單位圓上不同的點，記
OA
=
a
，
OB
=
b
，
OC
=
c
．
（ⅰ）當
a
⊥
b
時，求S（
c
，
a
）+S（
c
，
b
）的最大值；
（ⅱ）寫出S（
a
，
b
）+S（
b
，
c
）+S（
c
，
a
）的最大值．（只需寫出結果）
組卷：360引用：8難度：0.3
解析