2022-2023學(xué)年貴州省黔南州高三（上）質(zhì)檢數(shù)學(xué)試卷（文科）

一、選擇題：本大題共12小題，每小題5分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

• 1．已知全集U={1，2，3，4，5}，集合M={1，2}，N={3，4}，則?_U（M∪N）=（　　）

  A．{5}

  B．{1，2}

  C．{3，4}

  D．{1，2，3，4}
  組卷：3729引用：39難度：0.9

  解析

• 2．設(shè)z=i（2+i），則

  z

  =（　　）

  A．1+2i

  B．-1+2i

  C．1-2i

  D．-1-2i
  組卷：4078引用：17難度：0.9

  解析

• 3．下列函數(shù)中，在區(qū)間（0，+∞）上單調(diào)遞增的是（　　）

  A．y= x 1 2

  B．y=2-x

  C．y=lo g 1 2 x

  D．y= 1 x
  組卷：4036引用：23難度：0.9

  解析

• 4．已知單位向量

  a

  ，

  b

  的夾角為60°，則在下列向量中，與

  b

  垂直的是（　　）

  A． a + 2 b

  B．2 a + b

  C． a -2 b

  D．2 a - b
  組卷：6357引用：31難度：0.8

  解析

• 5．在“一帶一路”知識(shí)測(cè)驗(yàn)后，甲、乙、丙三人對(duì)成績(jī)進(jìn)行預(yù)測(cè)．
  甲：我的成績(jī)比乙高．
  乙：丙的成績(jī)比我和甲的都高．
  丙：我的成績(jī)比乙高．
  成績(jī)公布后，三人成績(jī)互不相同且只有一個(gè)人預(yù)測(cè)正確，那么三人按成績(jī)由高到低的次序?yàn)椋ā　。?/h2>

  A．甲、乙、丙

  B．乙、甲、丙

  C．丙、乙、甲

  D．甲、丙、乙
  組卷：2211引用：33難度：0.6

  解析

• 6．函數(shù)y=2^|x|sin2x的圖象可能是（　　）

  A．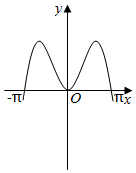

  B．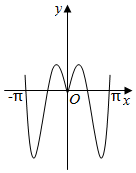

  C．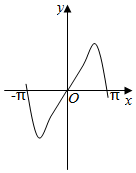

  D．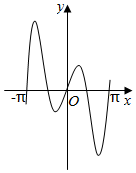
  組卷：8040引用：113難度：0.7

  解析

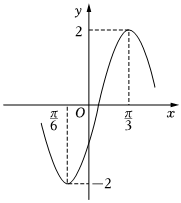• 7．已知函數(shù)f（x）=Asin（ωx+φ）（A＞0，ω＞0，

  |

  φ

  |

  ＜

  π

  2

  ）的部分圖像如圖所示，則函數(shù)f（x）的解析式為（　　）

  A． y = 2 sin （ 2 x - π 3 ）	B． y = 2 sin （ 2 x - π 6 ）
  C． y = 2 sin （ x + π 6 ）	D． y = 2 sin （ x + π 3 ）
  組卷：197引用：2難度：0.6

  解析

請(qǐng)考生在第22、23題中任選一題作答，如果多做，則按所做的第一題記分，作答時(shí)用2B鉛筆在答題卡上把所選題目對(duì)應(yīng)題號(hào)的方框涂黑．選修4—4：坐標(biāo)系與參數(shù)方程

• 22．已知曲線C₁，C₂的參數(shù)方程分別為C₁：

  x = 2 cos 2 θ

  y = 2 sin 2 θ

  （θ為參數(shù)），C₂：

  x = t + 1 t

  y = t - 1 t

  （t為參數(shù)）．
  （1）將C₁，C₂的參數(shù)方程化為普通方程．
  （2）以坐標(biāo)原點(diǎn)為極點(diǎn)，x軸正半軸為極軸建立極坐標(biāo)系，設(shè)C₁，C₂的交點(diǎn)為P，求圓心在極軸上，且經(jīng)過(guò)極點(diǎn)和點(diǎn)P的圓的極坐標(biāo)方程．
  組卷：136引用：3難度：0.6

  解析

選修4—5：不等式選講

• 23．已知a,b,c∈R₊，且a+b+c=1．證明：
  （Ⅰ）a²+b²+c²≥

  1

  3

  ；
  （Ⅱ）

  a

  2

  b

  +

  b

  2

  c

  +

  c

  2

  a

  ≥1．
  組卷：273引用：5難度：0.5

  解析