2022年山西省晉中市高考數學模擬試卷（理科）（5月份）

一、選擇題：本大題共12小題.每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知a∈R，（2+ai）i=1+2i（i為虛數單位），則a等于（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：25引用：2難度：0.8

  解析

• 2．設集合A={x|x²-x-12≤0}，

  B

  =

  {

  x

  |

  1

  16

  ＜

  2

  x

  ＜

  4

  }

  ，則A∪B等于（　　）

  A．（-3，4]

  B．[-3，2）

  C．（-4，4]

  D．[-3，4]
  組卷：46引用：2難度：0.8

  解析

• 3．設向量

  a

  ，

  b

  滿足

  |

  a

  |

  =

  2

  ，

  |

  a

  -

  b

  |

  =

  3

  ，

  a

  與

  b

  的夾角為

  π

  3

  ，則

  |

  b

  |

  等于（　　）

  A．2

  B．1

  C．3

  D． 2
  組卷：170引用：2難度：0.8

  解析

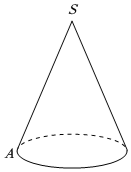• 4．如圖，已知圓錐的母線長SA=3，一只螞蟻從A點出發繞著圓錐的側面爬行一圈回到點A的最短距離為

  3

  3

  ，則該圓錐的底面半徑為（　　）

  A．1

  B．2

  C． 2

  D． 3
  組卷：251引用：4難度：0.6

  解析

• 5．我國古代數學巨著《九章算術》第三章中“衰分”介紹了比例分配問題，“衰分”是指按比例遞減分配的意思，通常稱遞減的比例為“衰分比”．如甲、乙、丙三人分配獎金的衰分比為20%，若甲分得獎金10000元，則乙、丙分得獎金分別為8000元和6400元．現有三名技術人員A，B，C攻克了一項技術難題．若A，B，C按照一定的“衰分比”分配獎金共75880元，其中A拿到了28000元，則“衰分比”為（　　）

  A．20%

  B．15%

  C．25%

  D．10%
  組卷：16引用：2難度：0.8

  解析

• 6．北京2022年冬奧會吉祥物“冰墩墩”和冬殘奧會吉祥物“雪容融”一亮相，好評不斷，這是一次中國文化與奧林匹克精神的完美結合．某商場決定派小王和小高等7名志愿者將兩個吉祥物安裝在大廣場上，每人參與且只參與一個吉祥物的安裝，每個吉祥物都至少由三名志愿者安裝，若小王和小高必須安裝不同的吉祥物，則不同的分配方案種數為（　　）

  A．40

  B．30

  C．20

  D．80
  組卷：65引用：1難度：0.8

  解析

• 7．若tanθ=-1，則

  cosθ

  （

  1

  -

  sin

  2

  θ

  ）

  sinθ

  -

  cosθ

  等于（　　）

  A． 1 2

  B．2

  C．-1

  D． - 1 3
  組卷：259引用：2難度：0.7

  解析

（二）選考題：共10分.考生從22、23題中任選一題作答，如果多做，則按所做的第一題計分.作答時用2B鉛筆在答題卡上將所選題目對應的題號涂黑.

• 22．在平面直角坐標系xOy中，直線l的參數方程為

  x = - 2 + tcosφ

  y = - 3 + tsinφ

  （t為參數，φ∈[0，π）），以坐標原點為極點，x軸正半軸為極軸，建立極坐標系，圓C的極坐標方程為

  ρ

  =

  4

  cos

  （

  θ

  +

  π

  3

  ）

  ．
  （1）求圓C的直角坐標方程；
  （2）設

  P

  （

  -

  2

  ，-

  3

  ）

  ，若直線l與圓C相交于A，B兩點，求

  |

  PA

  -

  PB

  |

  的最大值．
  組卷：18引用：2難度：0.5

  解析

• 23．已知a＞0，b＞0，且a+2b=3．
  （1）若

  1

  a

  +

  9

  2

  b

  ≥

  |

  x

  +

  2

  |

  恒成立，求x的取值范圍；
  （2）證明：

  （

  1

  a

  +

  4

  b

  ）

  （

  a

  3

  +

  b

  3

  ）

  ≥

  9

  ．
  組卷：56引用：3難度：0.5

  解析