試卷征集
          
                
          
            
          
            
          
                
          
                    
                    
          加入會員
          
                
          
            
          
            
          
                
          
                    
                    
          操作視頻
          
                
          
            
          
        
          
    
          

    
          
        
    
          
    
          
    
          
        
          
            



          
    當前位置：
    試卷中心
    >
    試卷詳情

          


          
    
          
        
          
            2022-2023學年山東省淄博實驗中學、齊盛高級中學高一（下）期中數學試卷
        
          
        
          
            發布：2024/5/25 8:0:9
        
          
            
          一、單項選擇題，本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．
          
            
            
                    
          • 
                        
            1．已知復數
            z
            =
            2
            -
            ai
            1
            -
            2
            i
            （其中i是虛數單位）是純虛數，則實數a的值是（　　）
            組卷：56引用：3難度：0.7
            
                    
            • 
                    
          • 
                        
            2．
            tan
            （
            -
            7
            π
            6
            ）
            =（　　）
            組卷：414引用：3難度：0.8
            
                    
            • 
                    
          • 
                        
            3．已知向量
            a
            ，
            b
            不共線，且
            c
            =λ
            a
            +
            b
            ，
            d
            =
            a
            +（2λ-1）
            b
            ，若
            c
            與
            d
            共線反向，則實數λ值為（　　）
            組卷：559引用：9難度：0.9
            
                    
            • 
                    
          • 
                        
            4．下列說法中，正確的是（　　）
            組卷：123引用：5難度：0.7
            
                    
            • 
                    
          • 
                        
            5．已知向量
            a
            、
            b
            不共線，若
            AB
            =
            a
            +2
            b
            ，
            BC
            =-4
            a
            -
            b
            ，
            CD
            =-5
            a
            -3
            b
            ，則四邊形ABCD是（　　）
            組卷：362引用：7難度：0.9
            
                    
            • 
                    
          • 
                        
            6．已知sin（α-
            π
            6
            ）=
            1
            3
            ，則sin（2
            α
            +
            π
            6
            ）=（　　）
            組卷：611引用：11難度：0.8
            
                    
            • 
                    
          • 
                        
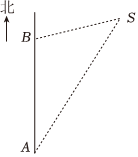            7．如圖，一艘船向正北方向航行，航行速度為每小時
            10
            39
            海里，在A處看燈塔S在船的北偏東
            θ
            （
            sinθ
            =
            3
            4
            ）
            的方向上．1小時后，船航行到B處，在B處看燈塔S在船的北偏東3θ的方向上，則船航行到B處時與燈塔S之間的距離為（　　）
            組卷：486引用：21難度：0.8
            
                    
            • 
            
          
        
            
          四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．
          
            
            
                    
          • 
                        
            21．函數
            f
            （
            x
            ）
            =
            A
            sin
            （
            ωx
            +
            φ
            ）
            （
            A
            ＞
            0
            ，
            ω
            ＞
            0
            ，
            0
            ＜
            φ
            ＜
            π
            2
            ）
            在一個周期內的圖象如圖所示，
            （
            0
            ，
            3
            2
            ）
            與
            （
            π
            3
            ，
            3
            2
            ）
            為該圖象上兩點，且函數f（x）的一個零點為
            -
            π
            12
            ．
            （1）求f（x）的解析式；
            （2）將y=f（x）的圖象向左平移
            π
            6
            個單位長度，再將得到的圖象橫坐標不變，縱坐標變為原來的
            1
            3
            ，得到y=g（x）的圖象．令F（x）=f（x）g（x），求F（x）的最大值，若F（x）取得最大值時x的值為x0，求tan4x0．
            組卷：59引用：2難度：0.5
            
                    
            • 
                    
          • 
                        
            22．已知函數
            f
            （
            x
            ）
            =
            sin
            （
            x
            -
            π
            3
            ）
            -
            2
            3
            si
            n
            2
            （
            x
            2
            -
            π
            6
            ）
            +
            3
            ．
            （1）求函數f（x）的最小正周期；
            （2）常數ω＞0，若函數y=f（ωx）在區間
            [
            -
            π
            2
            ，
            2
            π
            3
            ]
            上是增函數，求ω的取值范圍；
            （3）若函數
            g
            （
            x
            ）
            =
            1
            2
            [
            f
            （
            2
            x
            ）
            +
            af
            （
            x
            ）
            -
            af
            （
            π
            2
            -
            x
            ）
            -
            a
            ]
            -
            1
            在
            [
            -
            π
            4
            ，
            π
            2
            ]
            的最大值為2，求實數a的值．
            組卷：91引用：2難度：0.4
            
                    
            • 
            
          
    
          

    

          


        
          
    
          
    
          
         
          APP開發者：深圳市菁優智慧教育股份有限公司| 應用名稱：菁優網 | 應用版本：5.0.7 |隱私協議|第三方SDK|用戶服務條款
          本網部分資源來源于會員上傳，除本網組織的資源外，版權歸原作者所有，如有侵犯版權，請立刻和本網聯系并提供證據，本網將在三個工作日內改正