2022-2023學年安徽省宣城六中九年級（上）第二次月考數學試卷

一、單選題（共10小題，每題4分，共40分）

• 1．下列運算正確的是（　　）

  A．x2?x4=x6	B．（x2）4=x6
  C．x3+x3=2x6	D．（-2x）3=-6x3
  組卷：584引用：7難度：0.7

  解析

• 2．北京冬奧村是2022年北京冬季奧運會冬殘奧會最大的非競賽類場館之一，總建筑面積約38.66萬平方米，其中38.66萬用科學記數法可表示為（　　）

  A．0.3866×106

  B．3.9×105

  C．3.866×105

  D．38.66×105
  組卷：127引用：3難度：0.8

  解析

• 3．如圖，菱形OABC在平面直角坐標系中的位置如圖所示，∠AOC=45°，OA=2，則點C的坐標為（　　）

  A．（ 2 ，1）

  B．（ 2 ， 2 ）

  C．（1， 2 ）

  D．（ 2 +1，1）
  組卷：1114引用：6難度：0.5

  解析

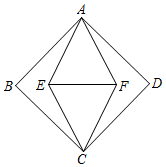• 4．如圖，正方形ABCD的面積為8，菱形AECF的面積為4，則EF的長是（　　）

  A．4

  B． 5

  C．2

  D．1
  組卷：1137引用：14難度：0.7

  解析

• 5．小兵在暑假調查了某工廠得知，該工廠2020年全年某產品的產量為234萬噸，經該廠的技術人員預計2022年全年該產品的產量為345萬噸，設2020年至2022年該產品的預計年平均增長率為x,根據題意列出方程得（　　）

  A．234（1+x）2=345	B．234（1-2x）=345
  C．234（1+2x）=345	D．234（1-x）2=345
  組卷：792引用：8難度：0.6

  解析

• 6．關于函數y=2（x+3）²+1，下列說法：①函數的最小值為1；②函數圖象的對稱軸為直線x=3；③當x≥0時，y隨x的增大而增大；④當x≤0時，y隨x的增大而減小．其中正確的有（　　）個．

  A．1

  B．2

  C．3

  D．4
  組卷：482引用：6難度：0.6

  解析

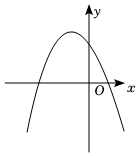• 7．二次函數y=ax²+bx+c的圖象如圖所示，則一次函數y=-bx+c的圖象不經過（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：432引用：5難度：0.7

  解析

七、（本題滿分12分）

• 22．【經典回顧】
  梅文鼎是我國清初著名的數學家，他在《勾股舉隅》中給出多種證明勾股定理的方法．圖1是其中一種方法的示意圖及部分輔助線．
  在△ABC中，∠ACB=90°，四邊形ADEB、ACHI和BFGC分別是以Rt△ABC的三邊為一邊的正方形．延長IH和FG，交于點L，連接LC并延長交DE于點J，交AB于點K，延長DA交IL于點M．
  （1）證明：AD=LC；
  （2）證明：正方形ACHI的面積等于四邊形ACLM的面積；
  （3）請利用（2）中的結論證明勾股定理．
  【遷移拓展】
  （4）如圖2，四邊形ACHI和BFGC分別是以△ABC的兩邊為一邊的平行四邊形，探索在AB下方是否存在平行四邊形ADEB，使得該平行四邊形的面積等于平行四邊形ACHI、BFGC的面積之和．若存在，作出滿足條件的平行四邊形ADEB（保留適當的作圖痕跡）；若不存在，請說明理由．
  
  組卷：1901引用：4難度：0.1

  解析

八、（本題滿分14分）

• 23．已知二次函數y=-ax²+2ax+2（a≠0）．
  （1）求二次函數圖象的對稱軸；
  （2）若該二次函數的圖象開口向上，當-1≤x≤5時，函數圖象的最高點為M，最低點為N，點M的縱坐標為

  19

  2

  ，求點M和點N的坐標；
  （3）在（2）的條件下，對直線MN下方二次函數圖象上的一點P，若S_△PMN=3，求點P的坐標．
  組卷：171引用：1難度：0.5

  解析