2021-2022學年山東省濟寧市嘉祥三中九年級（下）開學數學試卷

一．選擇題（每題3分，共30分）

• 1．如圖，在△ABC中，∠C=90°，AB=5，AC=4，下列三角函數表示正確的是（　　）

  A． sin A = 4 5

  B． cos A = 4 5

  C． tan A = 4 3

  D． tan B = 4 5
  組卷：939引用：5難度：0.7

  解析

• 2．反比例函數y=

  k

  -

  3

  x

  的圖象的兩個分支上，y都隨x的增大而減小，則k的取值范圍是（　　）

  A．k＜3

  B．k＞0

  C．k＞3

  D．k＜0
  組卷：115引用：2難度：0.7

  解析

• 3．一元二次方程3x²-6x-1=0的一次項系數、常數項分別是（　　）

  A．3，1

  B．3，-1

  C．-6，1

  D．-6，-1
  組卷：128引用：6難度：0.8

  解析

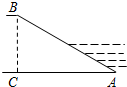• 4．如圖，河堤橫斷面迎水坡AB的坡度是1：2，坡面AB=

  6

  5

  ，則堤高的高度是（　　）

  A．3

  B． 6 5

  C．6

  D． 3 5
  組卷：343引用：4難度：0.7

  解析

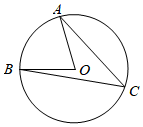• 5．如圖，點A，B，C是⊙O上的三個點，若∠AOB=76°，則∠C的度數為（　　）

  A．24°

  B．33°

  C．38°

  D．76°
  組卷：731引用：6難度：0.5

  解析

• 6．如圖，在2×2的正方形網格中有9個格點，已經取定點A和B，在余下的7個點中任取一點C，使△ABC為直角三角形的概率是（　　）

  A． 3 7

  B． 4 7

  C． 5 7

  D． 6 7
  組卷：247引用：3難度：0.6

  解析

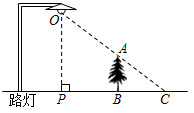• 7．如圖，小樹AB在路燈O的照射下形成投影BC．若樹高AB=2m,樹影BC=3m,樹與路燈的水平距離BP=4.5m.則路燈的高度OP為（　　）

  A．3m

  B．4m

  C．4.5m

  D．5m
  組卷：2254引用：27難度：0.5

  解析

三．解答題（共7小題，共55分）

• 21．閱讀材料：各類方程的解法不盡相同，但是它們有一個共同的基本數學思想——轉化，把未知轉化為已知．用“轉化”的數學思想，我們還可以解一些新的方程．例如，一元三次方程x³-2x²-3x=0，通過因式分解可以把它轉化為x（x²-2x-3）=0，解方程x=0和x²-2x-3=0，可得方程x³-2x²-3x=0的解．
  問題：（1）方程x³-2x²-3x=0的解是x₁=0，x₂=

  ，x₃=

  ．
  （2）求方程x³=6x²+16x的解．
  拓展：（3）用“轉化”思想求方程

  -

  2

  x

  +

  15

  =x的解．
  組卷：153引用：7難度：0.4

  解析

• 22．在平面直角坐標系中，二次函數y=ax²+bx+2的圖象與x軸交于A（-3，0），B（1，0）兩點，與y軸交于點C．
  （1）求這個二次函數的解析式；
  （2）點Q是線段AC上方的拋物線上一動點，過點Q作QE垂直于x軸，垂足為E．是否存在點Q，使以點B、Q、E為頂點的三角形與△AOC相似？若存在，求出點Q的坐標；若不存在，說明理由；
  （3）點M為拋物線上一動點，在x軸上是否存在點Q，使以A，C、M、Q為頂點的四邊形是平行四邊形？若存在，直接寫出點Q的坐標；若不存在，說明理由．
  
  組卷：290引用：1難度：0.2

  解析