2022-2023學年吉林省長春市榆樹市八號鎮三校聯考七年級（下）月考數學試卷（4月份）

一．選擇題（共8小題，每題3分共24分）

• 1．下列方程中，是一元一次方程的是（　　）

  A．2x=5

  B．x+y=2

  C．x2-2x=1

  D．xy=2
  組卷：18引用：3難度：0.9

  解析

• 2．已知△ABC的三個內角度數比為2：3：4，則這個三角形是（　　）

  A．銳角三角形

  B．直角三角形

  C．鈍角三角形

  D．無法確定
  組卷：86引用：5難度：0.6

  解析

• 3．下列正多邊形中，能夠鋪滿地面的是（　　）

  A．正五邊形

  B．正六邊形

  C．正八邊形

  D．正十二邊形
  組卷：215引用：8難度：0.7

  解析

• 4．若x＜y,則下列不等式一定成立的是（　　）

  A．-2x＜-2y

  B．x-2＜y-2

  C．mx＞my

  D． x 2 ＞ y 2
  組卷：1140引用：19難度：0.8

  解析

• 5．下列變形正確的是（　　）

  A．由4x-5=3x+2得4x-3x=-2+5

  B．由 2 3 x-1= 1 2 x+3得4x-1=3x+3

  C．由3（x-1）=2（x+3）得3x-1=2x+6

  D．由-2x=-3得x= 3 2
  組卷：17引用：2難度：0.9

  解析

• 6．在一次防疫知識競賽中，共有20道題，規定每答對一題得10分，答錯或不答都扣5分，小明得分要不小于120分，他至少要答對多少道題？若設小明答對x道題，則下列所列不等式正確的是（　　）

  A．10x-5（20-x）＞120	B．10x-5（20-x）＜120
  C．10x-5（20-x）≤120	D．10x-5（20-x）≥120
  組卷：92引用：2難度：0.7

  解析

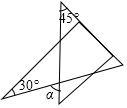• 7．將一副直角三角板按如圖所示的位置放置，使含30°角的三角板的一條直角邊和含45°角的三角板的一條直角邊放在同一條直線上，則∠α的度數是（　　）

  A．45°

  B．60°

  C．75°

  D．85°
  組卷：7189引用：71難度：0.9

  解析

• 8．當三角形中一個內角β是另外一個內角α的

  1

  2

  時，我們稱此三角形為“友好三角形”．如果一個“友好三角形”中有一個內角為54°，那么這個“友好三角形”的“友好角α”的度數為（　　）

  A．108°或27°	B．108°或54°
  C．27°或54°或108°	D．54°或84°或108°
  組卷：1142引用：9難度：0.5

  解析

三、解答題（78分）

• 24．【結論探究】如圖1，在△ABC中，∠ABC的平分線BP與外角∠ACD的平分線CP相交于點P，則有結論：∠P=

  1

  2

  ∠A．
  請完成上述結論的證明過程：
  ∵BP平分∠ABC，
  ∴∠PBC=

  1

  2

  ∠

  ．
  ∵CP平分∠ACD，
  ∴∠PCD=

  1

  2

  ∠ACD．
  ∵∠ACD=∠

  +∠ABC，
  ∴∠A=∠ACD-∠ABC，
  ∵∠PCD=∠P+∠PBC，
  ∴∠P=∠PCD-∠PBC=

  1

  2

  ∠ACD-

  1

  2

  ∠

  =

  1

  2

  ∠A．
  請直接應用上面的結論解決下面問題：
  【結論應用】如圖2，在△ABC中，∠A=70°，∠ABC的平分線BE與外角∠ACD的平分線CE相交于點E，外角∠HBC的平分線BF與EC的延長線相交于點F，求∠F的度數．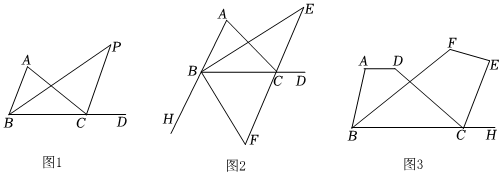
  
  【拓展應用】
  如圖3，已知四邊形ABCD與四邊形BCEF，BF平分角∠ABC，CE平分外角∠DCH．
  ①若∠A=100°，∠D=142°，則∠E+∠F=

  °；
  ②若∠A+∠D=α，∠E+∠F=β，則α=

  （用含β的代數式表示）．
  組卷：327引用：2難度：0.5

  解析

• 25．如圖，點C在線段AB上，AC=6cm,CB=4cm.點M以1cm/s的速度從點A沿線段AC向點C運動；同時點N以2cm/s的速度從點C出發，在線段CB上做往返運動（即沿C→B→C→B→…運動），當點M運動到點C時，點M、N都停止運動．設點M運動的時間為t（s）．
  
  （1）當t=1時，求MN的長．
  （2）當點C為線段MN的中點時，求t的值．
  （3）若點P是線段CN的中點，在整個運動過程中，是否存在某個時間段，使PM的長度保持不變？如果存在，求出PM的長度并寫出其對應的時間段；如果不存在，請說明理由．
  組卷：178引用：4難度：0.4

  解析