2023年江西省萍鄉(xiāng)市中考數(shù)學(xué)二模試卷

一、單項(xiàng)選擇題。(本大題共6小題,每小題3分,共18分）

• 1．下列各數(shù)中是無(wú)理數(shù)的是（　　）

  A．0

  B．1.5

  C． 3

  D．-2
  組卷：21引用：1難度：0.8

  解析

• 2．下列各式運(yùn)算正確的是（　　）

  A．a(chǎn)3?a3=2a3

  B．2a2+a2=3a2

  C．a(chǎn)9÷a3=a3

  D．7ab-5a=2
  組卷：28引用：1難度：0.7

  解析

• 3．如圖是一個(gè)底面為矩形、一條側(cè)棱垂直于底面的四棱錐（《九章算術(shù)》中稱為“陽(yáng)馬”），則它的左視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：215引用：2難度：0.8

  解析

• 4．一組數(shù)據(jù)1，2，3，4，5，x中存在唯一眾數(shù)，且該組數(shù)據(jù)的平均數(shù)等于眾數(shù)，則x的值為（　　）

  A．1

  B．3

  C．4

  D．5
  組卷：123引用：1難度：0.7

  解析

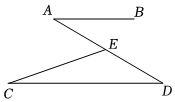• 5．如圖，已知AB∥CD，點(diǎn)E在線段AD上（不與點(diǎn)A，點(diǎn)D重合），連接CE．若∠C=20°，∠AEC=50°，則∠A=（　　）

  A．10°

  B．20°

  C．30°

  D．40°
  組卷：1298引用：36難度：0.7

  解析

• 6．如圖，在平面直角坐標(biāo)系中，已知點(diǎn)P（0，2），點(diǎn)A（4，2）．以點(diǎn)P為旋轉(zhuǎn)中心，把點(diǎn)A按逆時(shí)針?lè)较蛐D(zhuǎn)60°，得點(diǎn)B．在M₁（-

  3

  3

  ，0），M₂（-

  3

  ，-1），M₃（1，4），M₄（2，

  11

  2

  ）四個(gè)點(diǎn)中，直線PB經(jīng)過(guò)的點(diǎn)是（　　）

  A．M1

  B．M2

  C．M3

  D．M4
  組卷：1672引用：8難度：0.5

  解析

二、填空題。(本大題共6小題,每小題3分,共18分）

• 7．若

  x

  -

  1

  有意義，則x的取值范圍是

  ．
  組卷：1259引用：39難度：0.8

  解析

• 8．體現(xiàn)我國(guó)先進(jìn)核電技術(shù)的“華龍一號(hào)”，年發(fā)電能力相當(dāng)于減少二氧化碳排放16320000噸，數(shù)16320000用科學(xué)記數(shù)法表示為

  ．
  組卷：161引用：7難度：0.8

  解析

五、解答題。(本大題2小題,每題9分,共18分)

• 23．若二次函數(shù)y=ax²+bx+c的圖象經(jīng)過(guò)點(diǎn)A（-2，0），B（0，-4），其對(duì)稱軸為直線x=1，與x軸的另一交點(diǎn)為C．
  （1）求二次函數(shù)的表達(dá)式；
  （2）若點(diǎn)M在直線AB上，且在第四象限，過(guò)點(diǎn)M作MN⊥x軸于點(diǎn)N．
  ①若點(diǎn)N在線段OC上，且MN=3NC，求點(diǎn)M的坐標(biāo)；
  ②以MN為對(duì)角線作正方形MPNQ（點(diǎn)P在MN右側(cè)），當(dāng)點(diǎn)P在拋物線上時(shí)，求點(diǎn)M的坐標(biāo)．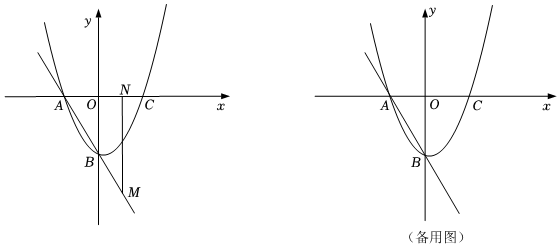
  
  組卷：2973引用：8難度：0.1

  解析

六、解答題。(本大題12分)

• 24．綜合與實(shí)踐
  數(shù)學(xué)是以數(shù)量關(guān)系和空間形式為主要研究對(duì)象的科學(xué)，數(shù)學(xué)實(shí)踐活動(dòng)有利于我們?cè)趫D形運(yùn)動(dòng)變化的過(guò)程中去發(fā)現(xiàn)其中的位置關(guān)系和數(shù)量關(guān)系，讓我們?cè)趯W(xué)習(xí)與探索中發(fā)現(xiàn)數(shù)學(xué)的美，體會(huì)數(shù)學(xué)實(shí)踐活動(dòng)帶給我們的樂(lè)趣．
  轉(zhuǎn)一轉(zhuǎn)：如圖①，在矩形ABCD中，點(diǎn)E、F、G分別為邊BC、AB、AD的中點(diǎn)，連接EF、DF，H為DF的中點(diǎn)，連接GH，將△BEF繞點(diǎn)B旋轉(zhuǎn)，線段DF、GH和CE的位置和長(zhǎng)度也隨之變化．當(dāng)△BEF繞點(diǎn)B順時(shí)針旋轉(zhuǎn)90°時(shí)，請(qǐng)解決下列問(wèn)題：
  （1）圖②中，AB=BC，此時(shí)點(diǎn)E落在AB的延長(zhǎng)線上，點(diǎn)F落在線段BC上，連接AF，猜想GH與CE之間的數(shù)量關(guān)系，并證明你的猜想；
  （2）圖③中，AB=2，BC=3，則

  GH

  CE

  =

  ，請(qǐng)證明你的結(jié)論；
  （3）當(dāng)AB=m,BC=n時(shí)，

  GH

  CE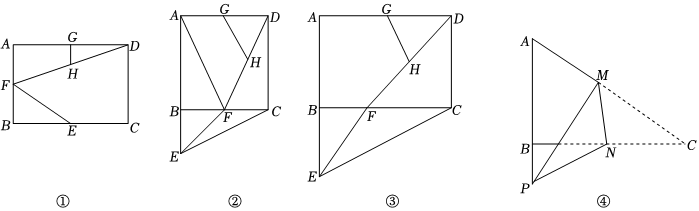

  =

  ；
  
  剪一剪、折一折：
  （4）在（2）的條件下，連接圖③中矩形的對(duì)角線AC，并沿對(duì)角線AC剪開(kāi)，得△ABC（如圖④）點(diǎn)M、N分別在AC、BC上，連接MN，將△CMN沿MN翻折，使點(diǎn)C的對(duì)應(yīng)點(diǎn)P落在AB的延長(zhǎng)線上，若PM平分∠APN，則CM長(zhǎng)為

  ．
  組卷：457引用：2難度：0.1

  解析