2022-2023學年山東省青島二十六中九年級(下)質檢數學試卷
發布:2024/4/20 14:35:0
一、單選題(本題滿分24分,共有8道小題,每小題3分)請將1—8各小題所選答案的標號涂寫在答題紙規定位置
-
1.下列四個數中,屬于有理數的是( )
A. 111B. 315C.π D.- 2組卷:519引用:9難度:0.7 -
2.萬花筒寫輪眼是漫畫《火影忍者》及其衍生作品中的一種瞳術,下列圖標中,是中心對稱圖形的有( )個.

A.2 B.3 C.4 D.5 組卷:254引用:3難度:0.9 -
3.下列計算正確的是( )
A.a+a2=a3 B.a6÷a3=a2 C.(-2x2)3=-8x6 D.(- )0+2-1=1212組卷:239引用:6難度:0.6 -
4.冠狀病毒因在顯微鏡下觀察類似王冠而得名,新型冠狀病毒是以前從未在人體中發現的冠狀病毒,新型冠狀病毒的半徑約是0.000000045米,將數0.000000045用科學記數法表示為( )
A.4.5×108 B.45×10-7 C.4.5×10-8 D.0.45×10-9 組卷:1442引用:22難度:0.8 -
5.某班有40人,一次體能測試后,老師對測試成績進行了統計.由于小亮沒有參加本次集體測試,因此計算其他39人的平均分為90分,方差s2=41.后來小亮進行了補測,成績為90分,關于該班40人的測試成績,下列說法正確的是( )
A.平均分不變,方差變大 B.平均分不變,方差變小 C.平均分和方差都不變 D.平均分和方差都改變 組卷:4832引用:51難度:0.5 -
 6.如圖,將一個規則幾何體的上半部分鉆一個圓孔,則該幾何體的俯視圖是( )
6.如圖,將一個規則幾何體的上半部分鉆一個圓孔,則該幾何體的俯視圖是( )A. 
B. 
C. 
D.  組卷:499引用:6難度:0.9
組卷:499引用:6難度:0.9 -
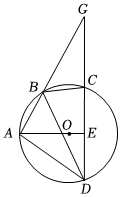 7.如圖,四邊形ABCD為⊙O的內接四邊形.弦AB與DC的延長線相交于點G,AO⊥CD,垂足為E,連接BD,∠GBC=48°,則∠DBC的度數為( )
7.如圖,四邊形ABCD為⊙O的內接四邊形.弦AB與DC的延長線相交于點G,AO⊥CD,垂足為E,連接BD,∠GBC=48°,則∠DBC的度數為( )A.84° B.72° C.66° D.48° 組卷:1640引用:10難度:0.7 -
8.在同一平面直角坐標系中,一次函數y=ax-b和二次函數y=-ax2-b的大致圖象是( )
A. 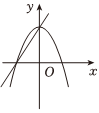
B. 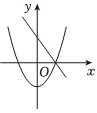
C. 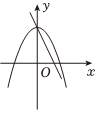
D. 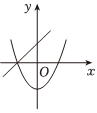 組卷:1290引用:13難度:0.7
組卷:1290引用:13難度:0.7
四、解答題(本題滿分74分,共有9道小題)
-
23.問題提出:已知矩形ABCD,點E為AB上的一點,EF⊥AB,交BD于點F.將△EBF繞點B順時針旋轉α(0°<α<90°)得到△E'BF',則AE'與DF'的有怎樣的數量關系.
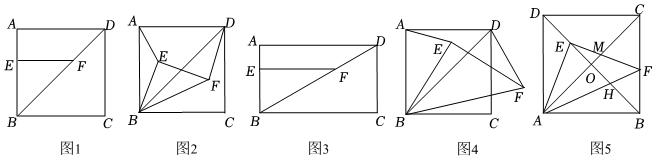
問題探究
探究一:如圖,已知正方形ABCD,點E為AB上的一點,EF⊥AB,交BD于點F.
(1)如圖1,直接寫出的值 ;DFAE
(2)將△EBF繞點B順時針旋轉到如圖2所示的位置,連接AE、DF,猜想DF與AE的數量關系,并證明你的結論;
探究二:如圖,已知矩形ABCD,點E為AB上的一點,EF⊥AB,交BD于點F.
如圖3,若四邊形ABCD為矩形,=ABBC,將△EBF繞點B順時針旋轉α(0o<α≤90o)得到△E'BF'(E、F的對應點分別為E'、F'點),連接AE'、DF',則22的值是否隨著α的變化而變化.若變化,請說明變化情況;若不變,請求出AE′DF′的值.AE′DF′
一般規律
如圖3,若四邊形ABCD為矩形,BC=mAB,其它條件都不變,將△EBF繞點B順時針旋轉α(0°<α<90°)得到△E'BF',連接AE',DF',請直接寫出AE'與DF'的數量關系.
問題解決
如圖4,當BE=BA時,其他條件不變,△EBF繞點B順時針旋轉,設旋轉角為α(0°<α<360°)當EA=ED時,直接寫出此時α=.
拓展延伸
如圖5,點E是正方形ABCD對角線BD上一點,連接AE,過點E作EF⊥AE,交線段BC于點F,交線段AC于點M,連接AF交線段BD于點H.給出下列四個結論,①AE=EF;②DE=CF;③S△AEM=S△MCF;④BE=DE+2BF;正確的結論有 個.2組卷:657引用:3難度:0.3 -
 24.已知:如圖,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.點D是BC中點,點P從點C出發,沿CA向點A勻速運動,速度為2cm/s;同時點Q從點A出發,沿AB向點B勻速運動,速度為3cm/s;連接PD,QD,PQ,將△PQD繞點D旋轉180°得△RTD,連接PT,QR.設運動時間為t(s)(0<t<3),解答下列問題:
24.已知:如圖,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.點D是BC中點,點P從點C出發,沿CA向點A勻速運動,速度為2cm/s;同時點Q從點A出發,沿AB向點B勻速運動,速度為3cm/s;連接PD,QD,PQ,將△PQD繞點D旋轉180°得△RTD,連接PT,QR.設運動時間為t(s)(0<t<3),解答下列問題:
(1)當t為何值時,RT∥BC?
(2)當t為何值時,四邊形PQRT是菱形?
(3)設四邊形PQRT的面積為y(cm2),求y與t的函數關系式;
(4)是否存在某一時刻t,使得點T在△ABC的外接圓上?若存在,求出t的值;若不存在,請說明理由.組卷:200引用:1難度:0.1


