2020-2021學年甘肅省平涼市靜寧一中實驗班高一(下)第三次月考數學試卷(理科)
發布:2024/5/23 8:0:8
一.選擇題(本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的)
-
1.已知數列{an}滿足an+an+2=2an+1(n∈N*),且a3=2,a5=8,則a7=( )
A.12 B.13 C.14 D.15 組卷:969引用:9難度:0.8 -
2.若直線l的方向向量為
,平面α的法向量為a,能使l∥α的是( )nA. =(1,0,0),a=(-2,0,0)nB. =(1,3,5),a=(1,0,1)nC. =(0,2,1),a=(-1,0,-1)nD. =(1,-1,3),a=(0,3,1)n組卷:1296引用:28難度:0.7 -
3.已知數列{an}的通項公式為an=26-2n,要使數列{an}的前n項和Sn,最大,則n的值為( )
A.14 B.13或14 C.12或11 D.13或12 組卷:59引用:5難度:0.7 -
4.已知
,a=(1,3),|b|=3,記|a+2b|=42與a夾角為θ,則cosb為( )(π2+2θ)A. -79B. -492C. 79D. 492組卷:420引用:3難度:0.5 -
5.已知x、y滿足不等式組
,設(x+2)2+(y+1)2的最小值為ω,則函數f(x)=sin(ωt+x≥0x-y≤04x+3y≤14)的最小正周期為( )π6A. 2π3B.π C. π2D. 2π5組卷:71引用:2難度:0.6 -
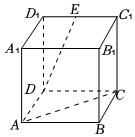 6.在如圖所示的正方體ABCD-A1B1C1D1中,E是C1D1的中點,則異面直線DE與AC所成角的余弦值為( )
6.在如圖所示的正方體ABCD-A1B1C1D1中,E是C1D1的中點,則異面直線DE與AC所成角的余弦值為( )A. 3510B. 105C. 55D. 1010組卷:57引用:5難度:0.6 -
7.在正項等比數列{an}中,a3a7=4,數列{log2an}的前9項之和為( )
A.11 B.9 C.15 D.13 組卷:135引用:8難度:0.5
三.解答題(共70分,解答應寫出文字說明、證明過程或演算步驟.)
-
21.已知函數
.f(x)=sinxsin(x+π6)+cos2(x-π12)-12
(1)求函數f(x)的單調遞減區間;
(2)已知銳角△ABC的內角A,B,C的對邊分別為a,b,c,且,f(B2)=32,求acosB-bcosC的取值范圍.b=3組卷:102引用:5難度:0.5 -
22.設數列{an}的前n項和為Sn,滿足:Sn=
,數列{bn}滿足:b1+3b2+32b3+…+3n-1bn=n(a1+an)2.n3
(1)求證:數列{an}為等差數列;
(2)若a1=1,a2=2,求數列的前n項和Tn.{anbn}組卷:180引用:2難度:0.6


