2022-2023學年黑龍江省大慶市龍鳳區九年級（下）期中數學試卷

一．選擇題（本大題共10小題，每題3分，共30分．）

• 1．在實數

  2

  ，

  1

  2

  ，0，-1中，最小的數是（　　）

  A．-1

  B．0

  C． 1 2

  D． 2
  組卷：841引用：15難度：0.9

  解析

• 2．下列垃圾分類標識圖案，既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：840引用：56難度：0.8

  解析

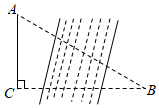• 3．如圖，某研究性學習小組為測量學校A與河對岸工廠B之間的距離，在學校附近選一點C，利用測量儀器測得∠A=60°，∠C=90°，AC=2km.據此，可求得學校與工廠之間的距離AB等于（　　）

  A．2km

  B．3km

  C． 2 3 km

  D．4km
  組卷：2120引用：27難度：0.7

  解析

• 4．如圖在三條橫線和三條豎線組成的圖形中，任選兩條橫線和兩條豎線都可以圍成一個矩形，從這些矩形中任選一個，則所選矩形含點A的概率是（　　）

  A． 1 4

  B． 1 3

  C． 3 8

  D． 4 9
  組卷：1717引用：18難度：0.5

  解析

• 5．某校為推薦一項作品參加“科技創新”比賽，對甲、乙、丙、丁四項候選作品進行量化評分，具體成績（百分制）如表：
  

  項目 作品	甲	乙	丙	丁
  創新性	90	95	90	90
  實用性	90	90	95	85

  如果按照創新性占60%，實用性占40%計算總成績，并根據總成績擇優推薦，那么應推薦的作品是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  組卷：1445引用：14難度：0.8

  解析

• 6．某市2018年底森林覆蓋率為63%．為貫徹落實“綠水青山就是金山銀山”的發展理念，該市大力開展植樹造林活動，2020年底森林覆蓋率達到68%，如果這兩年森林覆蓋率的年平均增長率為x,那么，符合題意的方程是（　　）

  A．0.63（1+x）=0.68	B．0.63（1+x）2=0.68
  C．0.63（1+2x）=0.68	D．0.63（1+2x）2=0.68
  組卷：1660引用：30難度：0.6

  解析

• 7．定義運算：m☆n=mn²-mn-1．例如：4☆2=4×2²-4×2-1=7，則方程1☆x=0的根的情況為（　　）

  A．有兩個不相等的實數根	B．有兩個相等的實數根
  C．無實數根	D．只有一個實數根
  組卷：2995引用：60難度：0.8

  解析

• 8．若菱形的周長為16，高為2，則菱形兩鄰角的度數之比為（　　）

  A．4：1

  B．5：1

  C．6：1

  D．7：1
  組卷：1290引用：11難度：0.7

  解析

• 9．關于x的分式方程

  ax

  -

  3

  x

  -

  2

  +1=

  3

  x

  -

  1

  2

  -

  x

  的解為正數，且使關于y的一元一次不等式組

  3 y - 2 2 ≤ y - 1

  y + 2 ＞ a

  有解，則所有滿足條件的整數a的值之和是（　　）

  A．-5

  B．-4

  C．-3

  D．-2
  組卷：2890引用：10難度：0.5

  解析

三、解答題（共10小題，滿分66分）

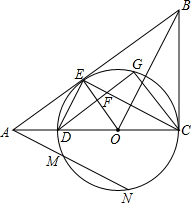• 27．如圖所示：⊙O與△ABC的邊BC相切于點C，與AC、AB分別交于點D、E，DE∥OB．DC是⊙O的直徑．連接OE，過C作CG∥OE交⊙O于G，連接DG、EC，DG與EC交于點F．
  （1）求證：直線AB與⊙O相切；
  （2）求證：AE?ED=AC?EF；
  （3）若EF=3，tan∠ACE=

  1

  2

  時，過A作AN∥CE交⊙O于M、N兩點（M在線段AN上），求AN的長．
  組卷：1621引用：4難度：0.1

  解析

• 28．如圖1，拋物線y=ax²+（a+3）x+3（a≠0）與x軸交于點A（4，0），與y軸交于點B，在x軸上有一動點E（m,0）（0＜m＜4），過點E作x軸的垂線交直線AB于點N，交拋物線于點P，過點P作PM⊥AB于點M．
  （1）求a的值和直線AB的函數表達式；
  （2）設△PMN的周長為C₁，△AEN的周長為C₂，若

  C

  1

  C

  2

  =

  6

  5

  ，求m的值；
  （3）如圖2，在（2）條件下，將線段OE繞點O逆時針旋轉得到OE′，旋轉角為α（0°＜α＜90°），連接E′A、E′B，求E′A+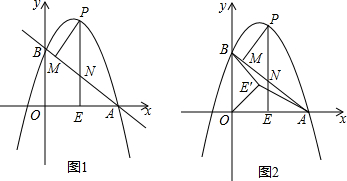

  2

  3

  E′B的最小值．
  
  組卷：7453引用：17難度：0.1

  解析