2014-2015學年學而思九年級（上）開學培優檢測試卷（十）

一、選擇題

• 1．

  4

  的值是（　　）

  A．4

  B．±2

  C．2

  D．-2
  組卷：118引用：7難度：0.9

  解析

• 2．若式子

  1

  -

  m

  在實數范圍內有意義，則m的取值范圍是（　　）

  A．m≥1

  B．m＞1

  C．m≤1

  D．m＜1
  組卷：91引用：1難度：0.9

  解析

• 3．下列計算正確的是（　　）

  A． 3 × 27 =3 3

  B． 7 3 = 7 3

  C． 40 - 10 = 10

  D． 25 x 3 =5x
  組卷：62引用：1難度：0.9

  解析

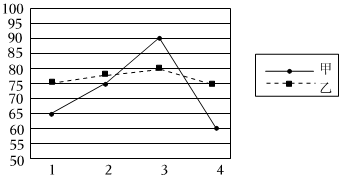• 4．如圖是甲、乙兩位同學某學期的四次數學考試成績的折線統計圖，則這四次數學考試成績中（　　）

  A．乙成績比甲成績穩定

  B．甲成績比乙成績穩定

  C．甲、乙兩成績一樣穩定

  D．不能比較兩人成績的穩定性
  組卷：161引用：31難度：0.9

  解析

• 5．一元二次方程x²-2x=0的根是（　　）

  A．x=2

  B．x=0

  C．x1=0，x2=2

  D．x1=0，x2=-2
  組卷：257引用：14難度：0.9

  解析

• 6．用配方法解方程x²-2x-5=0時，原方程應變形為（　　）

  A．（x+1）2=6

  B．（x+2）2=9

  C．（x-1）2=6

  D．（x-2）2=9
  組卷：3903引用：792難度：0.9

  解析

• 7．等腰三角形的底角為40°，則這個等腰三角形的頂角為（　　）

  A．40°

  B．80°

  C．100°

  D．100°或40°
  組卷：458引用：27難度：0.9

  解析

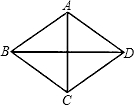• 8．在菱形ABCD中，兩條對角線AC=6，BD=8，則此菱形的邊長為（　　）

  A．5

  B．6

  C．8

  D．10
  組卷：252引用：26難度：0.9

  解析

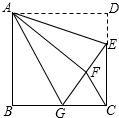• 9．如圖，正方形ABCD中，AB=6，點E在邊CD上，且CD=3DE．將△ADE沿AE對折至△AFE，延長EF交邊BC于點G，連接AG、CF．下列結論：①△ABG≌△AFG；②BG=GC；③AG∥CF；④S_△FGC=3．其中正確結論的個數是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：2724引用：85難度：0.5

  解析

三、解答題（本大題共有9小題，共76分．請在指定區域內作答，解答時應寫出文字說明、證明過程或演算步驟）

• 27．（1）如圖1，在正方形ABCD中，M是BC邊（不含端點B、C）上任意一點，P是BC延長線上一點，N是∠DCP的平分線上一點．若∠AMN=90°，求證：AM=MN．
  下面給出一種證明的思路，你可以按這一思路證明，也可以選擇另外的方法證明．
  證明：在邊AB上截取AE=MC，連接ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE．
  （下面請你完成余下的證明過程）
  （2）若將（1）中的“正方形ABCD”改為“正三角形ABC”（如圖2），N是∠ACP的平分線上一點，則∠AMN=60°時，結論AM=MN是否還成立？請說明理由．
  （3）若將（1）中的“正方形ABCD”改為“正n邊形ABCD…X，請你作出猜想：當∠AMN=

   

  時，結論AM=MN仍然成立．（直接寫出答案，不需要證明）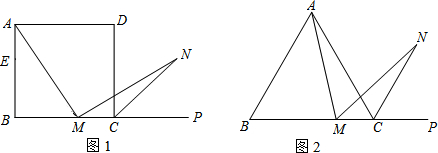
  
  組卷：1122引用：50難度：0.1

  解析

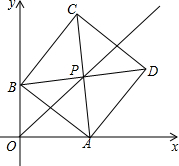• 28．在平面直角坐標系xOy中，邊長為

  2

  的正方形ABCD的對角線AC、BD相交于點P，頂點A在x軸正半軸上運動，頂點B在y軸正半軸上運動，頂點C、D都在第一象限．
  （1）當∠BAO=45°時，求點P的坐標；
  （2）求證：無論點A在x軸正半軸上、點B在y軸正半軸上怎樣運動，點P都在∠AOB的平分線上；
  （3）在運動的過程中，若點B與點O重合時，點P到y軸的距離是

  ，若點A與點O重合時，點P到y軸的距離是

  ．由此可見，點A、B在坐標軸的正半軸上運動（x軸的正半軸、y軸的正半軸都不包含原點O）時，點P到y軸的距離h的取值范圍是

  ．
  組卷：109引用：1難度：0.5

  解析