2023年湖北省荊門市龍泉中學(xué)高考數(shù)學(xué)模擬試卷（5月份）

一、單項選擇題：本題共8小題，每小題5分，共40分．出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={a,5-a,4}，B={3，2a+1}，A∪B={2，3，4，5}，則a=（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：64引用：3難度：0.7

  解析

• 2．已知復(fù)數(shù)iz=1+5i,則復(fù)數(shù)

  z

  +

  z

  =（　　）

  A．-10

  B．10

  C．-2

  D．2
  組卷：53引用：3難度：0.9

  解析

• 3．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的一條漸近線與直線2x-y+1=0垂直，則該雙曲線C的離心率為（　　）

  A． 5 2

  B． 3

  C．2

  D． 5
  組卷：210引用：3難度：0.7

  解析

• 4．某人周一至周五每天6：30至6：50出發(fā)去上班，其中在6：30至6：40出發(fā)的概率為0.4，在該時間段出發(fā)上班遲到的概率為0.1；在6：40至6：50出發(fā)的概率為0.6，在該時間段出發(fā)上班遲到的概率為0.2，則小王某天在6：30至6：50出發(fā)上班遲到的概率為（　　）

  A．0.3

  B．0.17

  C．0.16

  D．0.13
  組卷：147引用：2難度：0.7

  解析

• 5．已知點O為△ABC所在平面內(nèi)一點，在△ABC中，滿足

  2

  AB

  ?

  AO

  =

  |

  AB

  |

  2

  ，

  2

  AC

  ?

  AO

  =

  |

  AC

  |

  2

  ，則點O為該三角形的（　　）

  A．內(nèi)心

  B．外心

  C．垂心

  D．重心
  組卷：156引用：5難度：0.7

  解析

• 6．一個四棱錐的四個側(cè)面中，鈍角三角形最多有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：57引用：2難度：0.5

  解析

• 7．在我國古代，楊輝三角（如圖1）是解決很多數(shù)學(xué)問題的有力工具，從圖1中可以歸納出等式：

  C

  1

  1

  +

  C

  1

  2

  +

  C

  1

  3

  +

  ?

  +

  C

  1

  n

  =

  C

  2

  n

  +

  1

  、類比上述結(jié)論，借助楊輝三角解決下述問題：如圖2，該“芻童垛”共2021層，底層如圖3，一邊2023個圓球，另一邊2022個圓球，向上逐層每邊減少1個圓球，頂層堆6個圓球，則此“芻童垛”中圓球的總數(shù)為（　　）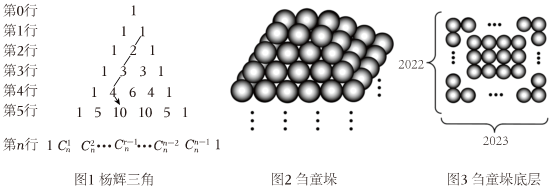
  

  A． 2 C 3 2023 - 2

  B． 2 C 3 2024 - 2

  C． C 4 2024 - 2

  D． C 4 2023 - 2
  組卷：75引用：5難度：0.7

  解析

四、解答題：共70分．解答應(yīng)寫出文字說明，證明過程或演算步驟．

• 21．設(shè)函數(shù)f（x）=e^x-ax,x≥0且a∈R．
  （1）求函數(shù)f（x）的單調(diào)性；
  （2）若f（x）≥x²+1恒成立，求實數(shù)a的取值范圍．
  組卷：357引用：8難度：0.4

  解析

• 22．已知橢圓E：

  x

  2

  4

  +

  y

  2

  2

  =

  1

  ．若直線l：

  x

  =

  my

  +

  2

  與橢圓E交于A、B兩點，交x軸于點F，點A，F(xiàn)，B在直線l′：

  x

  =

  2

  2

  上的射影依次為點D，K，G．
  （1）若直線l交y軸于點T，且

  TA

  =

  λ

  1

  AF

  ，

  TB

  =

  λ

  2

  BF

  ，當(dāng)m變化時，探究λ₁+λ₂的值是否為定值？若是，求出λ₁+λ₂的值；否則，說明理由；
  （2）連接AG，BD，試探究當(dāng)m變化時，直線AG與BD是否相交于定點？若是，請求出定點的坐標(biāo)，并給予證明：否則，說明理由．
  組卷：49引用：2難度：0.5

  解析