2022-2023學年江西省南昌外國語學校九年級（下）月考數學試卷（3月份）

一、單選題（共18分）

• 1．

  2

  +

  1

  的倒數是（　　）

  A． - 2 - 1

  B． 1 - 2

  C． 2 - 1

  D． 2 + 1
  組卷：472引用：3難度：0.8

  解析

• 2．已知a⁴+

  1

  a

  4

  =14，那么a²+

  1

  a

  2

  的值為（　　）

  A．4

  B．-4

  C．±4

  D．16
  組卷：577引用：4難度：0.7

  解析

• 3．如圖，是由27個相同的小立方塊搭成的幾何體，它的三個視圖是3×3的正方形，若拿掉若干個小立方塊（幾何體不倒掉），其三個視圖仍都為3×3的正方形，則最多能拿掉小立方塊的個數為（　　）
  

  A．10

  B．12

  C．15

  D．18
  組卷：951引用：2難度：0.5

  解析

• 4．如圖，在正方形ABCB₁中，

  AB

  =

  3

  ，AB與直線l所夾銳角為60°，延長CB₁交直線l于點A₁，作正方形A₁B₁C₁B₂，延長C₁B₂交直線l于點A₂，作正方形A₂B₂C₂B₃，延長C₂B₃交直線l于點A₃，作正方形A₃B₃C₃B₄ …，依此規律，則線段A₂₀₂₁A₂₀₂₂=（　　）

  A．2×（ 3 3 ）2019

  B．2×（ 3 3 ）2020

  C．2×（ 3 3 ）2021

  D．2×（ 3 3 ）2022
  組卷：89引用：1難度：0.6

  解析

• 5．我們平常用的是十進制，如2019=2×10³+0×10²+1×10¹+9，表示十進制的數要用10個數碼：0，1，2，3，4，5，6，7，8，9．在計算機中用的是二進制，只有兩個數碼：0，1．如二進制中111=1×2²+1×2¹+1相當于十進制中的7，又如：11011=1×2⁴+1×2³+0×2²+1×2¹+1相當于十進制中的27．那么二進制中的1101相當于十進制中的（　　）

  A．10

  B．11

  C．12

  D．13
  組卷：207引用：2難度：0.7

  解析

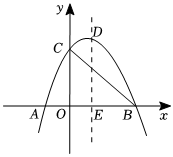• 6．如圖，拋物線y=ax²+bx+c與x軸交于點A（-1，0），B（3，0），交y軸的正半軸于點C，對稱軸交拋物線于點D，交x軸于點E，則下列結論：①b+2c＞0；②a+b≥am²+bm（m為任意實數）；③若點P為對稱軸上的動點，則|PB-PC|有最大值，最大值為

  c

  2

  +

  9

  ；④若m是方程ax²+bx+c=0的一個根，則一定有b²-4ac=（2am+b）² 成立，其中正確的序號有（　　）

  A．①②③④

  B．①②③

  C．③④

  D．①②④
  組卷：260引用：4難度：0.4

  解析

二、填空題?（共18分）

• 7．已知m,n是方程x²+2021x+7=0的兩個根，則（m²+2020m+6）（n²+2022n+8）=

  ．
  組卷：194引用：3難度：0.7

  解析

三、解答題?（共84分）

• 22．在平面直角坐標系中，O為坐標原點，拋物線y=ax²+2ax+c與x軸交于點A，B，與y軸交于點C，點A的坐標為（2，0），點

  D

  （

  -

  3

  ，

  5

  2

  ）

  在拋物線上．
  
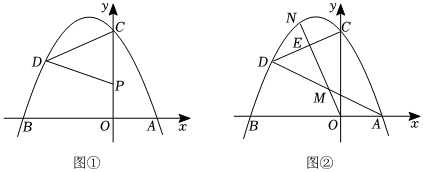
  （1）求拋物線的表達式；
  （2）如圖①，點P在y軸上，且點P在點C的下方，若∠PDC=45°，求點P的坐標；
  （3）如圖②，E為線段CD上的動點，射線OE與線段AD交于點M，與拋物線交于點N，求

  MN

  OM

  的最大值．
  組卷：1702引用：11難度：0.1

  解析

• 23．【閱讀感悟】數學解題的一個重要原則是對一個數學問題，改變它的形式，變換它的結構，直到發現有價值的東西．知識與方法上的類比是探索發展的重要途徑，是發現新問題、新結論的重要方法．
  
  【知識方法】
  （1）如圖1，在△ABC與△EDC中，∠ACB=∠ECD=90°，AC=BC，CE=CD，連接AE、BD，則AE與BD的數量關系是

  ；
  【類比遷移】
  （2）如圖2，正方形ABCD與正方形DEFG共用點D，連接AE、CG，試探究AE、CG之間的數量關系，并說明理由；
  （3）如圖3，在△ABC與△EDC是等邊三角形，△EDC可以繞點C旋轉，連接AE、AD、BD．若BC=6，當四邊形ADCE是平行四邊形時，則線段DE的長是

  ；
  【拓展應用】
  （4）如圖4，點P是矩形ABCD邊CD上的動點，連接BP，將BP繞點P順時針旋轉90°至EP，EP交AD于點G，將CP繞點P順時針旋轉90°至FP，連接FG、FA、AE、若AB=3，BC=6，求四邊形AEGF面積的最小值．
  組卷：345引用：2難度：0.4

  解析