當前位置：試卷中心 > 試卷詳情

2023-2024學年山東省棗莊八中東校區高二（上）開學摸底數學試卷

發布：2024/8/11 5:0:1

一、單項選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知復數z=
i
1
-
i
（i為虛數單位），則z的虛部為（　　）
A．
1
2
i
B．
-
1
2
i
C．
1
2
D．
-
1
2
組卷：41引用：5難度：0.9
解析
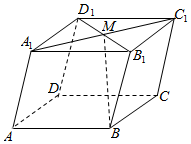2．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，M為A₁C₁，B₁D₁的交點．若
AB
=
a
，
AD
=
b
，
A
A
1
=
c
，則向量
BM
=（　　）
A．-
1
2
a
+
1
2
b
+
c
B．
1
2
a
+
1
2
b
+
c
C．-
1
2
a
-
1
2
b
+
c
D．
1
2
a
-
1
2
b
+
c
組卷：1921引用：49難度：0.7
解析
3．點A（3，4，5）關于坐標平面Oyz對稱的點B的坐標為（　　）
A．（3，4，-5） B．（-3，4，5） C．（-3，4，-5） D．（-3，-4，-5）
組卷：25引用：4難度：0.8
解析
4．已知正四棱錐的側棱長為
5
，高與斜高的夾角為30°，則該正四棱錐的體積為（　　）
A．
4
3
3
B．
2
3
3
C．
4
3
D．
2
3
組卷：120引用：3難度：0.5
解析
5．若
α
∈
（
0
，
π
2
）
，且
tan
2
α
=
cosα
2
-
sinα
，則sinα的值為（　　）
A．
15
4
B．
1
2
C．
1
3
D．
1
4
組卷：198引用：7難度：0.7
解析
6．若x,y,z∈R，則
x
2
+
y
2
+
z
2
+
x
2
+
y
2
+
（
z
-
1
）
2
+
（
x
-
1
）
2
+
（
y
-
1
）
2
+
z
2
+
（
x
-
1
）
2
+
（
y
-
1
）
2
+
（
z
-
1
）
2
的最小值為（　　）
A．2
2
B．3 C．2
3
D．4
組卷：91引用：3難度：0.5
解析
7．已知
|
a
|
=
1
，
b
=
（
1
，
3
）
，
a
⊥
（
a
+
b
）
，則向量
a
在向量
b
上的投影向量為（　　）
A．
（
-
1
，-
3
）
B．
（
-
3
，-
1
）
C．
（
-
1
2
，-
3
2
）
D．
（
-
1
4
，-
3
4
）
組卷：371引用：3難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

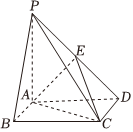21．如圖，在底面是矩形的四棱錐P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=4，E是PD的中點．
（1）求證：CD⊥平面PAD；
（2）求平面EAC與平面ACD夾角的余弦值；
（3）求B點到平面EAC的距離．
組卷：377引用：6難度：0.4
解析
22．已知甲、乙兩個袋子中各裝有形狀、大小、質地完全相同的3個紅球和3個黑球，現設計如下試驗：從甲、乙兩個袋子中各隨機取出1個球，觀察兩球的顏色，若兩球顏色不同，則將兩球交換后放回袋子中，并繼續上述摸球過程；若兩球顏色相同，則停止取球，試驗結束．
（1）求第1次摸球取出的兩球顏色不同的概率；
（2）我們知道，當事件A與B相互獨立時，有P（AB）=P（A）P（B）．那么，當事件A與B不獨立時，如何表示積事件AB的概率呢？某數學小組通過研究性學習發現如下命題：P（AB）=P（A）P（B|A），其中P（B|A）表示事件A發生的條件下事件B發生的概率，且對于古典概型中的事件A，B，有
P
（
B
|
A
）
=
n
（
AB
）
n
（
A
）
．依據上述發現，求“第2次摸球試驗即結束”的概率．
組卷：216引用：3難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2023-2024學年山東省棗莊八中東校區高二（上）開學摸底數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知復數z=i1-i（i為虛數單位），則z的虛部為（ ）

2．如圖，在平行六面體ABCD-A1B1C1D1中，M為A1C1，B1D1的交點．若AB=a，AD=b，AA1=c，則向量BM=（ ）

3．點A（3，4，5）關于坐標平面Oyz對稱的點B的坐標為（ ）

4．已知正四棱錐的側棱長為5，高與斜高的夾角為30°，則該正四棱錐的體積為（ ）

5．若α∈（0，π2），且tan2α=cosα2-sinα，則sinα的值為（ ）

6．若x,y,z∈R，則x2+y2+z2+x2+y2+（z-1）2+（x-1）2+（y-1）2+z2+（x-1）2+（y-1）2+（z-1）2的最小值為（ ）

7．已知|a|=1，b=（1，3），a⊥（a+b），則向量a在向量b上的投影向量為（ ）

四、解答題：本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

21．如圖，在底面是矩形的四棱錐P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=4，E是PD的中點．（1）求證：CD⊥平面PAD；（2）求平面EAC與平面ACD夾角的余弦值；（3）求B點到平面EAC的距離．

1．已知復數z=
i
1
-
i
（i為虛數單位），則z的虛部為（　　）

2．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，M為A₁C₁，B₁D₁的交點．若
AB
=
a
，
AD
=
b
，
A
A
1
=
c
，則向量
BM
=（　　）

3．點A（3，4，5）關于坐標平面Oyz對稱的點B的坐標為（　　）

4．已知正四棱錐的側棱長為
5
，高與斜高的夾角為30°，則該正四棱錐的體積為（　　）

5．若
α
∈
（
0
，
π
2
）
，且
tan
2
α
=
cosα
2
-
sinα
，則sinα的值為（　　）

6．若x,y,z∈R，則
x
2
+
y
2
+
z
2
+
x
2
+
y
2
+
（
z
-
1
）
2
+
（
x
-
1
）
2
+
（
y
-
1
）
2
+
z
2
+
（
x
-
1
）
2
+
（
y
-
1
）
2
+
（
z
-
1
）
2
的最小值為（　　）

7．已知
|
a
|
=
1
，
b
=
（
1
，
3
）
，
a
⊥
（
a
+
b
）
，則向量
a
在向量
b
上的投影向量為（　　）

21．如圖，在底面是矩形的四棱錐P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=4，E是PD的中點．
（1）求證：CD⊥平面PAD；
（2）求平面EAC與平面ACD夾角的余弦值；
（3）求B點到平面EAC的距離．