2022-2023學(xué)年湖南省湘潭市、衡陽市、邵陽市三市教研聯(lián)考高一（下）期中數(shù)學(xué)試卷

一、單選題（本大題共8小題，共40分。在每小題列出的選項中，選出符合題目的一項）

• 1．已知復(fù)數(shù)z滿足（1+i）z=3-i,則z的虛部為（　　）

  A．2

  B．-2

  C．2i

  D．-2i
  組卷：36引用：2難度：0.8

  解析

• 2．已知a＞0，b＞0，且a+2b=1，則

  1

  a

  +

  1

  b

  的最小值為（　　）

  A． 2

  B． 1 2

  C．3-2 2

  D．3+2 2
  組卷：364引用：7難度：0.8

  解析

• 3．已知正六邊形ABCDEF中，

  AB

  +

  CD

  +

  EF

  =（　　）

  A． AF

  B． BE

  C． CD

  D． 0
  組卷：1029引用：3難度：0.7

  解析

• 4．設(shè)a=lg2，b=cos2，c=2^0.2，則（　　）

  A．b＜c＜a

  B．c＜b＜a

  C．b＜a＜c

  D．a(chǎn)＜b＜c
  組卷：735引用：13難度：0.8

  解析

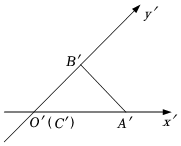• 5．如圖，水平放置的△ABC的斜二測直觀圖是圖中的△A'B'C'，若A'C'=2，A'B'=2，則△ABC的面積為（　　）

  A． 2 2

  B． 4 2

  C．8

  D． 8 2
  組卷：221引用：3難度：0.8

  解析

• 6．函數(shù)

  f

  （

  x

  ）

  =

  1

  2

  x

  -

  lo

  g

  2

  x

  +

  1

  的零點所在區(qū)間為（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（3，4）
  組卷：182引用：6難度：0.7

  解析

• 7．若△ABC為銳角三角形，則（　　）

  A．sinA＞sinB	B．cosA＞cosB
  C．sin（cosA）＞sin（sinB）	D．cos（cosA）＞cos（sinB）
  組卷：78引用：3難度：0.6

  解析

四、解答題（本大題共6小題，共70分。解答應(yīng)寫出文字說明，證明過程或演算步驟）

• 21．對于函數(shù)f（x），g（x），若存在實數(shù)k使得函數(shù)h（x）=kf（x）?g（x），那么稱函數(shù)h（x）為f（x），g（x）的k積函數(shù)．
  （1）設(shè)函數(shù)f（x）=sinx,

  g

  （

  x

  ）

  =

  cos

  （

  x

  +

  2

  π

  3

  ）

  ，

  h

  （

  x

  ）

  =

  2

  sin

  （

  2

  x

  -

  π

  3

  ）

  +

  3

  ，試判斷h（x）是否為f（x），g（x）的k積函數(shù)？若是，請求出k的值；若不是，請說明理由；
  （2）設(shè)函數(shù)

  f

  （

  x

  ）

  =

  mx

  +

  n

  x

  （其中m＞0，n＞0，x＞0），且函數(shù)f（x）圖象的最低點坐標(biāo)為（2，4），若函數(shù)g（x）=f（2-x），h（x）是f（x），g（x）的1積函數(shù)，且對于任意實數(shù)x∈（0，2），h（x）≥a恒成立，求實數(shù)a的取值范圍．
  組卷：32引用：3難度：0.5

  解析

• 22．在①（a+c）（sinA-sinC）=b（sinA-sinB）；②

  2

  b

  -

  a

  c

  -

  cos

  A

  cos

  C

  =

  0

  ；③向量

  m

  =

  （

  c

  ,

  3

  b

  ）

  與

  n

  =

  （

  cos

  C

  ，

  sin

  B

  ）

  平行，這三個條件中任選一個，補充在下面題干中，然后解答問題．
  已知△ABC內(nèi)角A，B，C的對邊分別為a,b,c,且滿足_______．
  （1）求角C；
  （2）若△ABC為銳角三角形，且a=4，求△ABC面積的取值范圍．
  組卷：283引用：5難度：0.5

  解析