2022-2023學年河南省南陽一中高一（下）第一次月考數學試卷

一、選擇題（共8小題，每小題5分，滿分40分）

• 1．1弧度的圓心角所對的弧長為6，則這個圓心角所夾的扇形的面積是（　　）

  A．3

  B．6

  C．18

  D．36
  組卷：130引用：3難度：0.7

  解析

• 2．若-

  π

  2

  ＜α＜0，則點P（tanα，cosα）位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：157引用：32難度：0.9

  解析

• 3．若|cosθ|=cosθ，|tanθ|=-tanθ，則

  θ

  2

  的終邊在（　　）

  A．第一、三象限

  B．第二、四象限

  C．第一、三象限或在x軸的非負半軸上

  D．第二、四象限或在x軸上
  組卷：23引用：1難度：0.7

  解析

• 4．函數

  y

  =

  sinx

  x

  2

  -

  x

  +

  log

  1

  2

  （

  x

  +

  4

  ）

  的定義域為（　　）

  A．（-4，-π]

  B．[-π，-3]

  C．[-3，0]

  D．（1，+∞）
  組卷：103引用：4難度：0.5

  解析

• 5．函數f（x）=

  sinx

  +

  x

  cosx

  +

  x

  2

  在[-π，π]的圖象大致為（　　）

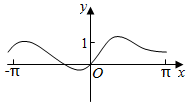
  A．	B．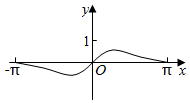
  C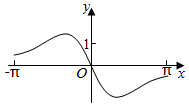．	D．
  組卷：9604引用：52難度：0.8

  解析

• 6．已知函數

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  -

  π

  3

  ）

  （

  1

  ＜

  ω

  ＜

  4

  ）

  滿足

  f

  （

  π

  6

  ）

  =

  0

  ，將函數f（x）圖象向左平移φ（φ＞0）個單位后其圖象關于y軸對稱，則φ的最小值為（　　）

  A． 5 π 12

  B． π 3

  C． π 4

  D． π 12
  組卷：149引用：3難度：0.7

  解析

• 7．設直線

  y

  =

  3

  3

  與函數y=sinx,y=cosx,y=tanx的圖像在

  （

  0

  ，

  π

  2

  ）

  內交點的橫坐標依次為x₁，x₂，x₃，則sin（x₁+x₂+x₃）=（　　）

  A． - 3 2

  B． - 1 2

  C． 1 2

  D． 3 2
  組卷：307引用：4難度：0.8

  解析

四、解答題（共6小題，滿分70分）

• 21．已知函數

  f

  （

  x

  ）

  =

  2

  sin

  （

  2

  x

  +

  π

  6

  ）

  +

  a

  +

  1

  （其中a為常數）．
  （1）求f（x）的單調區間；
  （2）若

  x

  ∈

  [

  0

  ，

  π

  2

  ]

  時，f（x）的最大值為4，求a的值；
  （3）求出使f（x）取得最大值時x的取值集合．
  組卷：79引用：1難度：0.7

  解析

• 22．已知點A（x₁，f（x₁）），B（x₂，f（x₂））是函數

  f

  （

  x

  ）

  =

  2

  sin

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，-

  π

  2

  ＜

  φ

  ＜

  0

  ）

  圖象上的任意兩點，且角φ的終邊經過點

  P

  （

  1

  ，-

  3

  ）

  ，若|f（x₁）-f（x₂）|=4時，|x₁-x₂|的最小值為

  π

  3

  ．
  （1）求函數f（x）的解析式；
  （2）求函數f（x）的對稱中心及在[0，π]上的減區間；
  （3）若方程3[f（x）]²-f（x）+m=0在

  x

  ∈

  （

  π

  9

  ，

  4

  π

  9

  ）

  內有兩個不相同的解，求實數m的取值范圍．
  組卷：108引用：5難度：0.5

  解析