2023-2024學(xué)年湖北省襄陽市名校高二（上）起點(diǎn)數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40.0分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．已知集合P={x|x²-x-2≤0}，Q={x|log₂（x-1）≤1}，則（?_RP）∩Q等于（　　）

  A．[2，3]	B．（-∞，-1]∪[3，+∞）
  C．（2，3]	D．（-∞，-1]∪（3，+∞）
  組卷：135引用：12難度：0.9

  解析

• 2．已知不重合的平面α、β、γ和直線l,則“α∥β”的充分不必要條件是（　　）

  A．α內(nèi)有無數(shù)條直線與β平行

  B．α內(nèi)的任何直線都與β平行

  C．α⊥γ且γ⊥β

  D．l⊥α且l⊥β
  組卷：33引用：7難度：0.7

  解析

• 3．如果函數(shù)y=x²+（1-a）x+2在區(qū)間（4，+∞）上單調(diào)遞增．那么實(shí)數(shù)a的取值范圍是（　　）

  A．（-∞，9]

  B．（-∞，-3]

  C．[5，+∞）

  D．（-∞，-7]
  組卷：159引用：7難度：0.7

  解析

• 4．在△ABC中，a=6，

  b

  =

  6

  3

  ，A=30°，則最長邊c=（　　）

  A．6

  B．12

  C．6或12

  D． 6 3
  組卷：125引用：5難度：0.6

  解析

• 5．已知向量

  a

  =（2，-3，1），

  b

  =（2，0，3），

  c

  =（0，0，2），則

  a

  ?（

  b

  +

  c

  ）=（　　）

  A．8

  B．9

  C．13

  D． 61
  組卷：204引用：9難度：0.9

  解析

• 6．二面角的棱上有A、B兩點(diǎn)，直線AC、BD分別在這個(gè)二面角的兩個(gè)半平面內(nèi)，且都垂直于AB，已知AB=2，AC=3，BD=4，

  CD

  =

  41

  ，則該二面角的大小為（　　）

  A．30°

  B．120°

  C．60°

  D．45°
  組卷：148引用：9難度：0.5

  解析

• 7．四面體ABCD的四個(gè)頂點(diǎn)都在球O的球面上，AB=BC=CD=DA=4，

  AC

  =

  BD

  =

  2

  2

  ，點(diǎn)E，F(xiàn)，G分別為棱BC，CD，AD的中點(diǎn)，現(xiàn)有如下結(jié)論：
  ①過點(diǎn)E，F(xiàn)，G作四面體ABCD的截面，則該截面的面積為2；
  ②四面體ABCD的體積為

  16

  3

  3

  ；
  ③過E作球O的截面，則截面面積的最大值與最小值的比為5：4．
  則上述說法正確的個(gè)數(shù)是（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：42引用：4難度：0.5

  解析

四、解答題：本大題共6小題，共70.0分。解答應(yīng)寫出文字說明，證明過程或演算步驟.

• 21．已知向量

  m

  =

  （

  2

  sinθ

  ，

  sinθ

  -

  cosθ

  ）

  ，

  n

  =

  （

  cosθ

  ，-

  2

  -

  m

  ）

  ，函數(shù)

  f

  （

  θ

  ）

  =

  m

  ?

  n

  的最小值為g（m）．
  （1）求g（m）；
  （2）函數(shù)h（x）為定義在R上的增函數(shù)，且對任意的x₁，x₂都滿足h（x₁+x₂）=h（x₁）+h（x₂），問：是否存在這樣的實(shí)數(shù)m,使不等式

  h

  （

  4

  sinθ

  -

  cosθ

  ）

  +

  h

  （

  2

  m

  +

  3

  ）

  ＞

  h

  （

  f

  （

  θ

  ）

  ）

  對所有

  θ

  ∈

  （

  π

  4

  ，

  π

  ）

  恒成立，若存在，求出m的取值范圍；若不存在，說明理由．
  組卷：51引用：7難度：0.3

  解析

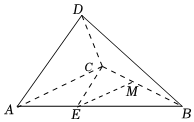• 22．如圖，在三棱錐D-ABC中，

  AD

  =

  CD

  =

  AE

  =

  CE

  =

  1

  2

  BC

  ，CD⊥AD，記二面角D-AC-B的平面角為θ．
  （1）若

  θ

  =

  π

  3

  ，BC=2，求三棱錐D-ABC的體積；
  （2）若M為BC的中點(diǎn)，求直線AD與EM所成角的取值范圍．
  組卷：204引用：5難度：0.4

  解析