2022-2023學年重慶市九龍坡區高一（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合U={x∈N|x≤7}，集合A={1，3，5，7}，B={1，2，4，7}，則（?_UA）∩（?_UB）=（　　）

  A．{2，4，6}

  B．{3，5，6}

  C．{0，6}

  D．{2，3，4，5，6}
  組卷：74引用：4難度：0.7

  解析

• 2．已知命題p：?x∈R，x²-2x+3＞0，則￢p是（　　）

  A．?x∈R，x2-2x+3＞0	B．?x∈R，x2-2x+3≤0
  C．?x∈R，x2-2x+3≤0	D．?x∈R，x2-2x+3＞0
  組卷：49引用：3難度：0.9

  解析

• 3．已知

  a

  =

  2

  2

  3

  ，

  b

  =

  lo

  g

  5

  2

  ，

  c

  =

  cos

  3

  ，則a、b、c的大小關系為（　　）

  A．a＞b＞c

  B．a＞c＞b

  C．b＞a＞c

  D．c＞a＞b
  組卷：101引用：4難度：0.9

  解析

• 4．某同學參加研究性學習活動，得到如下實驗數據：
  

  x	3	9	27	81
  y	2	3.1	4.1	5.2

  以下函數中最符合變量y與x的對應關系的是（　　）

  A． y = 1 9 x + 2	B． y = 4 9 x 2
  C． y = 1 4 × 2 x - 1 10	D．y=log3x+1
  組卷：25引用：1難度：0.7

  解析

• 5．若函數f（x）=lg（x²-ax+2）（a為常數）在（-∞，1]上單調遞減，則a∈（　　）

  A．[1，3）

  B．[1，+∞）

  C．[2，3）

  D．[2，+∞）
  組卷：122引用：1難度：0.6

  解析

• 6．函數

  y

  =

  |

  2

  x

  |

  ln

  1

  +

  x

  1

  -

  x

  在（-1，1）上的圖象大致為（　　）

  A．

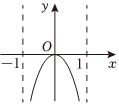
  B．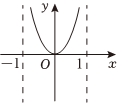

  C．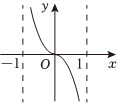

  D．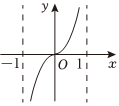
  組卷：86引用：5難度：0.7

  解析

• 7．中國茶文化博大精深，某同學在茶藝選修課中了解到，茶水的口感與茶葉類型和水的溫度有關，某種綠茶用80℃左右的水泡制可使茶湯清澈明亮，營養也較少破壞．為了方便控制水溫，該同學聯想到牛頓提出的物體在常溫環境下溫度變化的冷卻模型：如果物體的初始溫度是θ₁℃，環境溫度是θ₀℃，則經過t分鐘后物體的溫度θ℃將滿足

  θ

  =

  θ

  0

  +

  （

  θ

  1

  -

  θ

  0

  ）

  e

  -

  kt

  ，其中k是一個隨著物體與空氣的接觸狀況而定的正常數．該同學通過多次測量平均值的方法得到初始溫度為100℃的水在20℃的室溫中，12分鐘以后溫度下降到50℃．則在上述條件下，100℃的水應大約冷卻（　　）分鐘沖泡該綠茶（參考數據：ln2≈0.7，ln3≈1.1）

  A．3

  B．3.6

  C．4

  D．4.8
  組卷：70引用：2難度：0.6

  解析

四、解答題：本題共6個小題，共70分。解答應寫出文字說明，證明過程或演算步驟。

• 21．已知定義域為R的函數

  f

  （

  x

  ）

  =

  m

  -

  3

  x

  n

  +

  3

  x

  是奇函數．
  （1）求m,n的值；
  （2）判斷f（x）的單調性，并用定義證明；
  （3）若存在t∈[0，4]，使f（k-2t²）+f（4t-2t²）＜0成立，求k的取值范圍．
  組卷：108引用：4難度：0.6

  解析

• 22．已知函數f（x）在（-1，1）上有意義，且對任意x,y∈（-1，1）滿足

  f

  （

  x

  ）

  +

  f

  （

  y

  ）

  =

  f

  （

  x

  +

  y

  1

  +

  xy

  ）

  ．
  （1）求f（0）的值，判斷f（x）的奇偶性并證明你的結論；
  （2）若f（x）在（-1，1）上單調遞減，且

  f

  （

  -

  1

  2

  ）

  =

  1

  ，請問是否存在實數a,使得f（x）+f（a）+1≥0恒成立，若存在，給出實數a的一個取值；若不存在，請說明理由．
  組卷：136引用：3難度：0.5

  解析