當前位置：試卷中心 > 試卷詳情

2011年第九屆小學“希望杯”全國數學邀請賽試卷（六年級第2試）

發布：2024/4/20 14:35:0

1．計算：3.625+
0
.
?
4
?
5
-
1
4
11
=
．
組卷：134引用：3難度：0.9
解析
2．對于任意兩個數x和y,定義新運算◆和?，規則如下：
x◆y=
2
x
+
y
x
+
2
y
，x?y=
x
×
y
x
+
y
÷
3
；如1◆2=
2
×
1
+
2
1
+
2
×
2
，1?2=
1
×
2
1
+
2
3
=
6
5
=
1
1
5
，由此計算
0
.
?
3
?
6
◆
（
4
?
1
1
2
）
=
．
組卷：73引用：3難度：0.9
解析
3．用4根火柴，在桌面上可以拼成一個正方形；用13根火柴，可以拼成四個正方形；…如圖，拼成的圖形中，若最下面一層有15個正方形，則需要火柴
根．
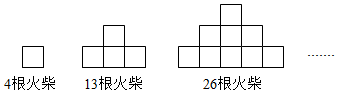組卷：35引用：3難度：0.9
解析
4．若自然數N可以表示城3個連續自然數的和，也可以表示成11個連續自然數的和，還可以表示成12個連續自然數的和，則N的最小值是
．（注：最小的自然數是0）
組卷：41引用：3難度：0.9
解析
5．十進制計數法，是逢10進1，如24₁₀=2×10+4×1，
36
5
10
=
3
×
1
0
2
+
6
×
10
+
5
×
1
；計算機使用的是二進制計數法，是逢2進1，如
7
10
=
1
×
2
2
+
1
×
2
+
1
×
1
=
11
1
2
，
1
2
10
=
1
×
2
3
+
1
×
2
2
+
0
×
2
+
0
×
1
=
110
0
2
，如果一個自然數可以寫成m進制數45_m，也可以寫成n進制數54_n，那么最小的m=
，n=
．（注：
a
n
=
a
×
a
×
a
×
…
×
a
n
個
a
）
組卷：172引用：4難度：0.5
解析

15．有8個足球隊進行循環賽，勝隊得1分，負隊得0分，平局的兩隊各得0.5分．比賽結束后，將各隊的得分按從高到低排名后發現：各隊得分互不相同，且第二名的得分與最后四名所得的總分一樣多．求這次比賽中，取得第二名的隊的得分．
組卷：69引用：2難度：0.3
解析
16．將兩個不同的自然數中較大的數換成他們的差，稱為一次操作，如此繼續下去，直到這兩個數相同為止．如對20和26進行這樣的操作，過程如下：
（20，26）→（20，6）→（14，6）→（8，6）→（2，6）→（2，4）→（2，2）
（1）對45和80進行上述操作．
（2）若對兩個四位數進行上述操作，最后得到的相同數是17．求這兩個四位數的和的最大值．
組卷：199引用：2難度：0.5
解析

1．計算：3.625+0.?4?5-1411=．