2022年天津市濱海新區(qū)七所重點(diǎn)學(xué)校高考數(shù)學(xué)聯(lián)考試卷（2月份）

一.選擇題：本題共9小題，每小題5分，共45分.在每小題給出的四個(gè)選項(xiàng)中只有一項(xiàng)是符合題目要求的，請(qǐng)將正確答案的序號(hào)填涂到答題卡上.

• 1．設(shè)全集U={-2，-1，0，1，2，3}，集合A={-1，0，1，3}，B={-2，0，2}，則A∩（?_UB）=（　　）

  A．{0，1，2}

  B．{-2，0，2}

  C．{0，2}

  D．{-1，1，3}
  組卷：107引用：2難度：0.8

  解析

• 2．設(shè)x∈R，則“（x-1）（x+2）≥0”是“|x-2|＜1”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：401引用：1難度：0.8

  解析

• 3．函數(shù)f（x）=

  2

  ln

  |

  x

  |

  2

  x

  +

  2

  -

  x

  的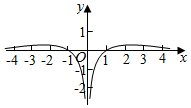大致圖象為（　　）

  A．	B．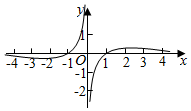
  C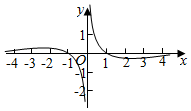．	D．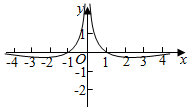
  組卷：355引用：7難度：0.8

  解析

• 4．下列說法不正確的是（　　）

  A．線性回歸直線方程 ? y = ? b x + ? a 一定過點(diǎn) （ x ， y ）

  B．?dāng)?shù)據(jù)x1，x2，…，xn的平均數(shù)為 x ，則2x1+2，2x2+2，…，2xn+2的平均數(shù)為 2 x + 2

  C．?dāng)?shù)據(jù)5，1，2，3，4，6的第40百分位數(shù)為2

  D．隨機(jī)變量X～N（μ，σ2），其正態(tài)曲線是單峰的，它關(guān)于直線x=μ對(duì)稱
  組卷：410引用：2難度：0.7

  解析

• 5．設(shè)函數(shù)f（x）在R上是偶函數(shù)，且在（-∞，0]上單調(diào)遞增，a=f（log_0.30.5），b=f（5^0.2），c=f（-lne），則（　　）

  A．b＜c＜a

  B．a(chǎn)＜c＜b

  C．a(chǎn)＜b＜c

  D．c＜b＜a
  組卷：186引用：2難度：0.8

  解析

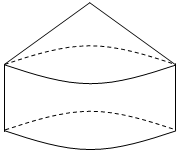• 6．如圖，圓錐的底面恰是圓柱的一個(gè)底面，圓柱的兩個(gè)底面分別為同一個(gè)球的兩個(gè)截面，且圓錐的頂點(diǎn)也在該球的球面上．若球的體積為36π，圓柱的高為2，則圓錐的體積為（　　）

  A．5π

  B． 5 3 π

  C．16π

  D． 16 3 π
  組卷：362引用：3難度：0.7

  解析

三.解答題：本大題共5小題，共75分.解答應(yīng)寫出文字說明，證明過程或演算步驟.

• 19．已知在各項(xiàng)均不相等的等差數(shù)列{a_n}中，a₁=1，且a₁，a₂，a₅成等比數(shù)列，數(shù)列{b_n}中，b₁=log₂（a₂+1），

  b

  n

  +

  1

  =

  4

  b

  n

  +

  2

  n

  +

  1

  ，n∈N*．
  （Ⅰ）求{a_n}的通項(xiàng)公式及其前n項(xiàng)和S_n；
  （Ⅱ）求證：

  {

  b

  n

  +

  2

  n

  }

  是等比數(shù)列，并求{b_n}的通項(xiàng)公式；
  （Ⅲ）設(shè)

  c

  n

  =

  a k b k + 2 k ， n = 2 k , k ∈ N *，

  3 × 2 k 4 b k - 2 k + 1 + 2 ， n = 2 k - 1 ， k ∈ N *，

  求數(shù)列{c_n}的前2n項(xiàng)的和T_2n．
  組卷：647引用：1難度：0.3

  解析

• 20．已知函數(shù)f（x）=-e^x-ax²（a∈R）．
  （Ⅰ）當(dāng)a=0時(shí)，求曲線y=f（x）在點(diǎn)（1，f（1））處的切線方程；
  （Ⅱ）當(dāng)a＞0時(shí)，若函數(shù)g（x）=xe^x+f（x），求g（x）的單調(diào)區(qū)間；
  （Ⅲ）當(dāng)a＞0時(shí)，若函數(shù)h（x）=f（x）+2e^x-ax恰有兩個(gè)不同的極值點(diǎn)x₁，x₂，且x₁＜x₂，求證：

  x

  1

  +

  x

  2

  2

  ＜

  ln

  2

  a

  ．
  組卷：454引用：2難度：0.3

  解析