2019-2020學年浙江省臺州市臨海市八年級（上）期末數學試卷
發布：2024/9/12 4:0:8
一、選擇題（本大題共10小題，每小題3分，共30分．請選出各題中一個符合題意的正確選項，不選、多選、錯選，均不給分）.
-
1．下列手機APP圖案中，屬于軸對稱圖形的是（ ）
組卷：15引用：1難度：0.7 -
2．現要用三根木棒搭一個三角形．已知其中兩根木棒的長分別是2cm和5cm,那么第三根的長可以是（ ）
組卷：16引用：1難度：0.7 -
3．如圖，人字梯中間一般都會設計一根拉桿，這樣做的幾何原理是（ ）組卷：38引用：3難度：0.6 -
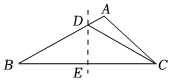4．如圖，DE是△ABC邊上的垂直平分線，∠A=110°，∠B=30°，則∠ACD的度數是（ ）組卷：41引用：2難度：0.7 -
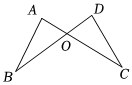5．如圖，線段AC與BD交于點O．現有四個條件：①OA=OD；②OB=OC；③AB=DC；④∠A=∠D．下列選項中不能判定△AOB≌△DOC的是（ ）組卷：29引用：2難度：0.6 -
6．下列計算結果為x7的是（ ）
組卷：24引用：1難度：0.7 -
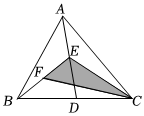7．如圖，在△ABC中，點D，E，F分別是BC，AD，BE的中點，若△CEF的面積為1，則△ABC的面積為（ ）組卷：120引用：2難度：0.7 -
8．甲，乙兩名學生參加校運會200米跑步比賽．甲在前半段的速度是每秒a米，后半段的速度是每秒b米（a＞b），共用時t1秒；乙以每秒
米的速度跑完全程，共用時t2秒．則t1和t2的大小關系為（ ）a+b2組卷：39引用：1難度：0.8
三、解答題（本大題共6小題，第21～23題每題6分，第24題8分，第25題12分，第26題12分，共50分）．
-
25．閱讀材料：我們知道，對一個圖形通過兩種不同的方法計算它的面積，可以得到一個數學等式．如圖①，將一個邊長為a的正方形紙片減去一個邊長為b的小正方形，根據剩下部分的面積，可以得到等式：a2-b2=a（a-b）+b（a-b），將等式右邊因式分解，即a2-b2=（a-b）（a+b）．
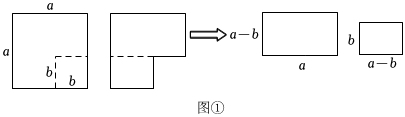
請類比上述探究過程，解答下列問題：
（1）如圖②，將一個棱長為a的正方體木塊挖去一個棱長為b的小正方體，根據剩下部分的體積，可以得到等式：，將等式右邊因式分解，即 ；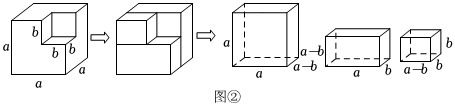
（2）類比以上探究過程，可得a3+b3=（ ）（ ）；
（3）根據以上探究的結果：
①計算：；（2019+1）3-（2019-1）3
②將y6-1因式分解成四個整式乘積的形式：
y6-1=（ ）（ ）（ ）（ ）．組卷：140引用：1難度：0.5 -
26．定義：連接三角形兩邊中點的線段叫做三角形的中位線．
性質：三角形的中位線平行于三角形的第三邊，并且等于第三邊的一半．
理解：如圖①，在△ABC中，點D，E分別是AB，AC的中點，那么DE為△ABC的一條中位線．可得DE∥BC且DE=BC．12
應用：如圖②，在△ABC中，AB=AC，點D，E分別在邊AB，AC上，且AD=AE．點M，N，P分別是DE，BC和CD的中點．已知∠BAC=α．
（1）當α=90°時，
①請直接寫出：PM與PN的數量關系 ；∠MPN=．
②是否存在點D，使得以P，M，N為頂點的三角形與△ADE全等？若存在，請求出點D的位置；若不存在，請說明理由．
（2）將△ADE繞點A旋轉，當點D在△ABC內時（如圖③），
①試說明PM與PN的數量關系，并求出∠MPN的度數（用含α的式子表示）；
②連接BD，MN，若AD=BD，直接寫出△ADE和△PMN的面積關系：．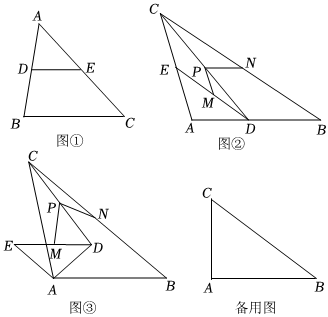
組卷：165引用：1難度：0.1