當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省蘇州市太倉市沙溪高級中學高一（下）調研數(shù)學試卷（4月份）

發(fā)布：2024/11/13 5:0:2

一、選擇題：在每小題給出的四個選項中，只有一項是符合題目要求的.本題共8小題，每小題5分，共40分

1．設復數(shù)z滿足（-1+i）z=1+3i,則z=（　　）
A．1+2i B．-2-2i C．1-2i D．2-2i
組卷：44引用：1難度：0.9
解析
2．已知向量
a
=
（
-
1
，
2
）
，
b
=
（
1
，-
2
λ
）
，若
（
a
+
3
b
）
∥
（
a
-
b
）
，則實數(shù)λ的值為（　　）
A．1 B．0 C．
4
3
D．
-
2
3
組卷：303引用：3難度：0.8
解析
3．
2
sin
50
°
-
cos
20
°
sin
20
°
=（　　）
A．-1 B．1 C．
-
3
D．
3
組卷：286引用：1難度：0.8
解析
4．下列說法中，正確的個數(shù)為（　　）
（1）有兩個面互相平行，其余各面都是平行四邊形的幾何體一定是棱柱
（2）有兩個面互相平行，其余四個面都是等腰梯形的六面體是棱臺；
（3）底面是等邊三角形，側面都是等腰三角形的三棱錐是正三棱錐；
（4）棱錐的側棱長與底面多邊形的邊長相等，則此棱錐可能是正六棱錐．
A．0個 B．1個 C．2個 D．3個
組卷：424引用：1難度：0.8
解析
5．已知
i
，
j
為互相垂直的單位向量，
a
=
-
i
+
2
j
，
b
=
3
i
-
（
λ
-
4
）
j
，且
a
與
a
-
b
的夾角為銳角，則λ的取值范圍為（　　）
A．（0，+∞） B．（0，10）∪（10，+∞）
C．（-∞，0） D．（-∞，-2）∪（-2，0）
組卷：169引用：1難度：0.7
解析
6．已知α∈（0，π），且
sinα
+
cosα
=
1
5
，則
sin
2
α
cos
2
α
-
sin
2
α
=（　　）
A．
24
7
B．12 C．
-
24
7
D．-12
組卷：349引用：3難度：0.7
解析
7．設
a
=
1
2
cos
10
°
-
3
2
sin
10
°
，
b
=
2
tan
12
°
1
+
tan
2
12
°
，
c
=
1
-
sin
40
°
2
，則a,b,c大小關系正確的是（　　）
A．a＜b＜c B．c＜b＜a C．a＜c＜b D．b＜c＜a
組卷：120引用：3難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．有一個半徑為r,圓心角
α
=
π
3
的扇形鐵皮OMN，現(xiàn)利用這塊鐵皮并根據(jù)下列方案之一，裁前出一個矩形．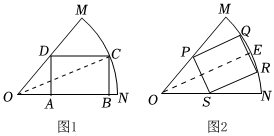

方案1：如圖1，裁前出的矩形ABCD的頂點A，B在線段ON上，點C在弧MN上，點D在線段OM上；
方案2：如圖2，裁剪出的矩形PQRS的頂點P，S分別在線段OM，ON上，頂點Q，R在弧MN上，并且滿足PQ∥RS∥OE，其中點E為弧MN的中點．
（1）按照方案1裁前，設∠NOC=θ，用θ表示矩形ABCD的面積，并求出其最大面積；
（2）按照方案2裁前，求矩形PQRS的最大面積，并與（1）中的結果比較后指出按哪種方案可以裁前出面積最大的矩形．
組卷：37引用：2難度：0.6
解析
22．在銳角△ABC中，
cos
B
=
2
2
，點O為△ABC的外心．
（1）若
BO
=
x
BA
+
y
BC
，求x+y的最大值；
（2）若
b
=
2
，
（i）求證：
OB
+
sin
2
A
?
OA
-
cos
2
A
?
OC
=
0
；
（ii）求
|
3
OB
+
2
OA
+
OC
|
的取值范圍．
組卷：94引用：1難度：0.4
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業(yè) 發(fā)布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（0，+∞）	B．（0，10）∪（10，+∞）
C．（-∞，0）	D．（-∞，-2）∪（-2，0）

2021-2022學年江蘇省蘇州市太倉市沙溪高級中學高一（下）調研數(shù)學試卷（4月份）

一、選擇題：在每小題給出的四個選項中，只有一項是符合題目要求的.本題共8小題，每小題5分，共40分

1．設復數(shù)z滿足（-1+i）z=1+3i,則z=（ ）

2．已知向量a=（-1，2），b=（1，-2λ），若（a+3b）∥（a-b），則實數(shù)λ的值為（ ）

3．2sin50°-cos20°sin20°=（ ）

5．已知i，j為互相垂直的單位向量，a=-i+2j，b=3i-（λ-4）j，且a與a-b的夾角為銳角，則λ的取值范圍為（ ）

6．已知α∈（0，π），且sinα+cosα=15，則sin2αcos2α-sin2α=（ ）

7．設a=12cos10°-32sin10°，b=2tan12°1+tan212°，c=1-sin40°2，則a,b,c大小關系正確的是（ ）

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

22．在銳角△ABC中，cosB=22，點O為△ABC的外心．（1）若BO=xBA+yBC，求x+y的最大值；（2）若b=2，（i）求證：OB+sin2A?OA-cos2A?OC=0；（ii）求|3OB+2OA+OC|的取值范圍．

1．設復數(shù)z滿足（-1+i）z=1+3i,則z=（　　）

2．已知向量
a
=
（
-
1
，
2
）
，
b
=
（
1
，-
2
λ
）
，若
（
a
+
3
b
）
∥
（
a
-
b
）
，則實數(shù)λ的值為（　　）

3．
2
sin
50
°
-
cos
20
°
sin
20
°
=（　　）

5．已知
i
，
j
為互相垂直的單位向量，
a
=
-
i
+
2
j
，
b
=
3
i
-
（
λ
-
4
）
j
，且
a
與
a
-
b
的夾角為銳角，則λ的取值范圍為（　　）

6．已知α∈（0，π），且
sinα
+
cosα
=
1
5
，則
sin
2
α
cos
2
α
-
sin
2
α
=（　　）

7．設
a
=
1
2
cos
10
°
-
3
2
sin
10
°
，
b
=
2
tan
12
°
1
+
tan
2
12
°
，
c
=
1
-
sin
40
°
2
，則a,b,c大小關系正確的是（　　）

22．在銳角△ABC中，
cos
B
=
2
2
，點O為△ABC的外心．
（1）若
BO
=
x
BA
+
y
BC
，求x+y的最大值；
（2）若
b
=
2
，
（i）求證：
OB
+
sin
2
A
?
OA
-
cos
2
A
?
OC
=
0
；
（ii）求
|
3
OB
+
2
OA
+
OC
|
的取值范圍．